Tras 6 semanas de terapia, la mejoría en cada paciente se comprueba. Esta mejoría es marcada (0-10) para cada paciente como sigue:
| Cognitiva | ..9.. | ..7.. | ..7.. | ..8.. | ..3.. | ..8.. | ..7.. | ..5.. | ..6.. | ..8.. |
| Psicodinámica | 3 | 2 | 4 | 0 | 5 | 2 | 4 | 3 | 2 | 5 |
Considerando normalidad e independencia y suponiendo las varianzas iguales, estimar la diferencia de medias en efectividad y calcular un intervalo de confianza al nivel 95%.
Recopilamos y obtenemos datos que nos serán de utilidad para posteriormente, resolver los distintos apartados.
Para obtener la media:
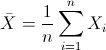
Por lo tanto:
· 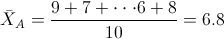
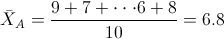
·
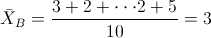
Para la cuasi desviación típica de cada muestra:
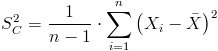
Para cada método, las desviaciones estándar son:
· S2cA ≈ 3.066667
· S2cB ≈ 2.444444
Para un 95%, obtenemos α:
100(1 - α) = 95
Despejamos el parámetro que nos interesa: α = 0.05.
Nos piden obtener un intervalo de confianza para la diferencia de medias de ambos métodos con las varianzas son desconocidas de ambas muestras e iguales.
Pasamos a confeccionar el intervalo de confianza para la diferencia de medias.
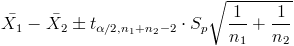
El siguiente paso es obtener los valores de:
· tα/2,n1+n2-2 = t0.05/2,10+10-2=t0.025, 18
Buscamos el valor en la tabla t-Student, y obtenemos: 2.1009.
Necesitamos obtener el valor de Sp:
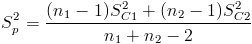
Sustituimos valores:
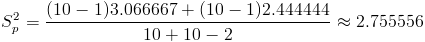
Ya disponemos todos los datos necesarios para obtener el intervalo bilateral de confianza al 95% de la diferencia de medias con varianzas desconocidas e iguales:
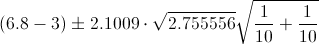
El intervalo de confianza bilateral al 95% es:
[2.240358, 5.359642]

No hay comentarios:
Publicar un comentario