Problema 6. Movimiento Parabólico.

Problema 6. En una feria, se gana un muñeco de peluche lanzando una moneda a un plato. El plato está en una repisa por encima del punto del lanzamiento de la moneda, y a una distancia horizontal de 2.1 metros de ese punto. Si un concursante, lanza la moneda con una velocidad de 6.4m/s, con un ángulo de 60º con la horizontal, la moneda caerá en el plato. Ignorando la fuerza del aire, calcular:

a) La altura del plato.

b) La velocidad en el momento justo antes de caer la moneda en el plato.

Antes que nada, hay que destacar, que el problema nos indica que no actúa la fuerza de rozamiento del aire, por lo que tomo el movimiento de forma idealizada.

Este problema, lo que plantea es que el concursante al tirar la moneda, describirá un movimiento parabólico, y con el ángulo dado de 60º, la moneda caerá en el plato.

Lo primero que tenemos que hacer, es escoger unos ejes de referencias apropiados.

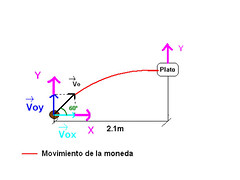
Figura 1.

Como se puede apreciar en la Figura 1, he escogido el eje de referencia en la monda justo en el instante de ser lanzada.

Al tener una velocidad inicial, ésta de descompondrá en sus proyecciones tanto en el eje “X” cómo en el eje “Y”.

Eje X:

Sustituimos valores:

Eje Y:

Sustituimos valores:

Es fácil observar que la moneda, describe un triángulo rectángulo con ángulo α.

Por lo tanto, por trigonometría, se puede calcular fácilmente cuanto vale el cateto opuesto:

Cateto opuesto = 2.1·tan60º

La distancia inicial del plato será el cateto opuesto del triángulo rectángulo.

Esta sería la distancia del plato, en caso que la moneda sólo se moviera en forma de recta, pero en la realidad, la moneda describe una parábola, por eso nos piden la altura real del plato.

Una vez planteado el problema, podemos calcular sus distintos apartados.

Apartado a)

En este apartado nos piden la altura del plato.

Para hallar esta altura, nos dan la distancia que dista el plato y la moneda, que es de 2.1 metros, deberemos saber en que instante de tiempo, la moneda recorre dicha distancia. Para ello nos basamos en la ecuación de posición de la moneda del eje “X”.

Sustituimos valores:

Se despeja el parámetro t, obteniendo:

t ≈ 0.66s

Por lo tanto, la moneda tardará 0.66 segundos en recorrer la distancia que la separa con el plato, 2.1 metros.

Una vez obtenido el instante de tiempo que recorre la distancia que dista del plato, para hallar la altura a la que s encuentra dicho plato, nos basamos en la ecuación de posición de la moneda en el eje “Y”

Sustituimos valores:

Por lo tanto, el plato está 1.52 metros por encima de la moneda.

Para comprobar nuestro resultado, y saber que realmente es así, podemos actuar de la siguiente manera.

El plato, lo consideramos que sólo tiene movimiento en una sola dirección, en este caso verticalmente, como me dice que siempre está en un punto fijo, no tiene velocidad inicial, por lo tanto, la ecuación que describe su movimiento, es la del movimiento de caída libre:

Sustituimos valores:

Una vez llegados a este punto, sabemos que la moneda recorre la distancia que dista del plato, 2.1 metros en un instante de tiempo de 0.66 segundos aproximadamente. Si el problema me indica que con un ángulo de 60º con la horizontal la moneda cae en el plato, significa, que en dicho instante de tiempo, la moneda y el plato se tocan, por lo que tienen la misma posición en el eje “Y”, es decir, la misma posición en la vertical.

Sabemos, que la ecuación que describe el movimiento de la moneda en el eje “Y” es la siguiente:

Por lo tanto, si en ese instante de tiempo que hemos calculado de 0.66 segundos tanto el plato como la moneda se tocan, significa que sus ecuaciones de posición en el eje “Y” deben ser iguales. Si qué igualo las ecuaciones de posición del plato y de la moneda en el instante de tiempo 0.66 segundos.

Sustituyo valores:

Operamos la igualdad anterior, obteniendo:

Por lo tanto obtenemos que:

3.66 ≈ 3.64

Esto quiere decir que son aproximadamente igual, no son exactamente iguales ya que en los cálculos previos se han tomado aproximaciones de los parámetros.

Pero una cosa si que es importante, y es que hemos demostrado que cuando el concursante lanza la moneda con un ángulo de 60º por encima de la horizontal, la moneda siempre contactará con el plato.

Apartado b)

Para hallar la velocidad, en su componente vertical, en el momento justo antes de caer el la moneda al plato, nos basamos en la ecuación de velocidad del eje “Y”, teniendo en cuenta, que la moneda tarda en recorrer la distancia que la separa con el plato en unos 0.66 segundos aproximadamente.

Sustituimos valores:

Tiene componente negativa, esto quiere decir que la moneda está ya bajando.