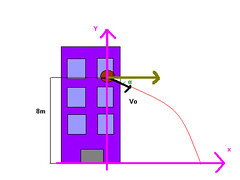
Problema 5. Movimiento Parabólico.

Problema 5. Un individuo lanza un globo de agua desde su ventana que dista del suelo en 8 metros. Cuando el globo abandona la mano del individuo, se mueve a 10m/s con un ángulo de 20º por debajo de la horizontal. ¿A qué distancia horizontal desde la ventana del individuo tocará el suelo el globo de agua? Ignore la resistencia del aire.

En este problema nos indican explícitamente que ignoremos la resistencia del aire, por lo que tomaremos cualquier movimiento como ideal.

Lo primero que hay que hacer es fijar unos ejes de coordenadas de referencias. En este caso, yo he tomado el eje de referencia en el suelo del pico, con su eje vertical “Y” hacia arriba, en sentido contrario al movimiento del globo de agua, y el eje horizontal “X” hacia la derecha, en sentido al movimiento del globo de agua.

Figura 1.

Al ser un movimiento bidimensional, el globo de agua describirá una parábola en su trayectoria.

Debemos obtener las proyecciones del vector velocidad en los ejes de coordenadas.

Eje X:

Sustituimos valores:



Eje Y:



Sustituimos valores:



Una vez planteado el problema, podemos proceder a resolverlo.

Nos piden la distancia que cae el globo de agua en el suelo, para ello debemos saber en que instante ocurre eso.

Para saber en que instante el globo cae al suelo, un dato importante es que su posición, con respecto al eje “Y”, es cero. Por lo tanto, nos basamos en la ecuación de la posición del eje “Y”:



Sustituimos valores.



Despejamos el parámetro t:

Resolvemos y obtenemos dos soluciones:

t1 ≈ -1.67s
t2 ≈ 0.98s

Al ser una ecuación cuadrática se obtienen dos valores para el parámetro t, la solución de valor negativa, no nos interesa ya que es un momento anterior, por lo tanto, el instante que el globo de agua cae al suelo es de 0.98 segundos después de su lanzamiento.

Una vez obtenido el instante donde el globo cae al suelo, vamos a resolver el dato que nos piden el problema, la distancia recorrida en ese instante.

Para ello nos basamos en la ecuación de posición del eje “X”:



Sustituimos valores:

x (0.98) = 10·cos(-20) ·0.98 ≈ 9.21m

Por lo tanto, el globo lleno de agua toca el suelo a una distancia de 9.21 metros de la ventana donde fue lanzado.