Problema 4. Movimiento Parabólico.

Problema 4. Para un proyectil lanzado con velocidad v0 y ángulo inicial α (entre 0º y 90º), calcular:

a) La expresión general de la altura máxima del proyectil.

b) El alcance horizontal.

Al no indicar fuerzas externas que intervengan en el movimiento del proyectil, asumimos que el movimiento que describe es ideal.

Para abordar este problema, lo primero que hay que haces, es fijar los ejes de referencias.

En este caso, he tomado el eje de referencia “Y” hacia arriba, mientras que el eje de referencia “X” hacia la derecha.

Y asumo que el proyectil al ser lanzado, se mueve hacia la derecha y de forma ascendente, es decir, en el instante inicial, se mueve en sentido de mis ejes de referencias.

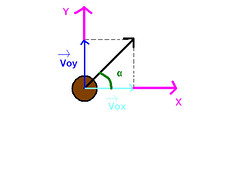
Figura 1.

Al ser un movimiento bidireccional, el vector velocidad inicial, tendrá proyecciones en los ejes de coordenadas de referencias que yo he tomado.

Eje X:

Eje Y:



Al escoger el eje de referencias en el momento justo antes de ser lanzado, sus posiciones iniciales tanto en el eje “X” como en el eje “Y” son cero.

Una vez plantado el problema, se puede resolver los apartados que nos piden.

Apartado a)

En este apartado nos piden la altura máxima alcanzada por el proyectil, para ello, nos basamos en la ecuación de posición del eje “Y”.

Eje Y: Movimiento uniformemente acelerado.



Sustituimos valores:



Hay que destacar, que la gravedad tiene sentido negativo, esto es así porque su sentido es el contrario al eje de referencia “Y” que yo he tomado.

Una vez tengamos la ecuación de su posición, debemos saber en que instante de tiempo, t, el proyectil alcanza su altura máxima.

Esto no es difícil saberlo, ya que cuando el proyectil tenga altura máxima, su velocidad será cero.
Por lo tanto, basándonos en la ecuación de velocidad en el eje “Y” obtenemos el instante de tiempo cuando la altura es máxima.



Sustituimos valores:



Despejamos el parámetro t:

Por lo tanto, en ese tiempo, la altura del proyectil será máxima.

Ahora, nos basamos en la ecuación de la posición del proyectil en el eje “Y”:

Y sustituimos el valor del instante t, cuando la altura sea máxima.

Operando obtenemos:

Por lo tanto, ésa será la altura máxima del proyectil para cualquier α dado.

El enunciado del problema, nos indica que el ángulo α puede estar comprendido entre 0º y 90º.

El valor de la altura máxima se obtiene cuando el término sen2α sea igual a uno, esto ocurre cuando α = 90º.

Esto quiere decir y como era de esperar, que el proyectil alcanzará su altura máxima cuando se lanza de forma verticalmente, por lo tanto no tiene proyecciones en el eje “X”.

Para demostrar lo dicho anteriormente, calculamos la distancia, en forma general, que recorre el proyectil cuando ha alcanzado su altura máxima.

Para este caso, debemos saber el instante que ocurre que el proyectil esté en su altura máxima. Este dato ya se calculó anteriormente, obteniéndose:

Nos basamos en la ecuación de posición del eje “X”:

Y sustituimos el tiempo donde la altura sea máxima:

Operando obtenemos:

Esa es la distancia que recorre el proyectil desde que se lanzó hasta que alcanza su altura máxima.

Para corroborar lo que hemos dicho anteriormente, de que la altura máxima se alcanza con α = 90º, es decir, cuando el movimiento es lanzado de forma verticalmente, sustituimos el valor de α = 90º en la relación de la distancia cuando alcanza su altura máxima.

Se puede observar, que la distancia recorrida es cero, por lo que su altura máxima es alcanzada cuando el proyectil es lanzado de forma vertical.

Apartado b)

En este apartado, nos piden la ecuación, en términos generales, de la distancia recorrida por un proyectil, desde que se lanza hasta que vuelve a caer al suelo.

Para este caso, cuando el proyectil cae al suelo, su posición, con respecto al eje “Y”, es cero. Por lo tanto podemos obtener el instante de tiempo cuando ocurre lo expuesto.

Nos basamos en la ecuación de posición del eje “Y”:

Sustituimos valores:



Operamos la relación anterior:



Por lo tanto, al ser una ecuación cuadrática, obtenemos dos soluciones:

t1 = 0.

El instante de cero segundos es justo en el momento de lanzar el proyectil, por lo que nuestra solución que nos interesa, es la t2.

Una vez obtenido el tiempo cuando el proyectil cae al suelo, hallamos la relación general de la distancia recorrida por el proyectil.

Para ello, nos basamos en la ecuación de posición del eje “X”.

Sustituimos el tiempo donde el proyectil cae al suelo:

Mediante relaciones trigonométricas obtenemos:

Esa es la distancia máxima de un proyectil para cualquier ángulo dado.

Para saber cual es su distancia máxima, se observa que el término sen2α debe ser igual a uno.

Para ello, obtenemos un valor de ángulo de 45º. Esto quiere decir, que la distancia del proyectil será máxima, cuando se lance con un ángulo inicial de 45º con la horizontal.