Problema14. VAD.

Ej14. Para cierta clase de flores, el 5% de las semillas no germinarán. Las semillas se empaquetan y venden en cajas de 10, con la garantía de que al menos nueve de ellas germinarán.

Encuentre la probabilidad de una caja cualquiera no cumpla la garantía.

Este problema es un claro ejemplo de “éxito” o “fracaso”, por lo tanto, se empleará la expresión de la distribución binomial para hallar la solución del problema.

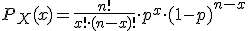
Donde:

p = 0.05: Probabilidad de éxito, la semilla no germinará.

n = 10: Número de cajas totales.

x: Depende de apartado, probabilidad de la variable aleatoria.

Se define la variable aleatoria:

X Ξ “Número semillas que no germinarán”.

El enunciado, nos pide hallar la probabilidad de que una caja cualquiera no cumpla las especificaciones.

Se sabe, que hay una garantía de que al menos 9 de cada 10 semillas germinarán de cada caja, es decir:

P(X) = P(X ≤ 1)

Esto es:

P(X) = P(X ≤ 1) = P(X = 0) + P(X = 1)

Se usa la expresión de la binomial, con x = 0, para obtener la probabilidad de todas las semillas germinan, obteniéndose:

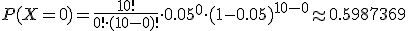
Se usa la expresión de la binomial, con x = 1, para obtener la probabilidad de una de las semillas no germina, obteniéndose:

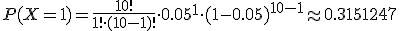
Por lo tanto, la probabilidad de que se cumpla la garantía es de:

P(X) = P(X ≤ 1) = P(X = 0) + P(X = 1) = 0.5987369 + 0.3151247 = 0.9138616

El enunciado, nos pide hallar la probabilidad de cuando no se cumple la garantía, por lo tanto, se usa la propiedad del complemento para obtener la solución del problema:

P(No se cumpla garantía) = 1 – P(X ≤ 1) = 1 – 0.9138616 = 0.0861384