Serie de Fibonacci

El fundamento de este capítulo es exponer el tema: La Serie de Fibonacci, usando como herramienta el lenguaje R.

Lo que se pretende es diseñar una función que devuelva dicha serie de longitud determinada por el usuario, pero antes de meternos en materia, un poco de historia.

La susodicha serie en cuestión, fue dada a conocer por Leonardo de Pisa, nuestro Fibonacci, gracias al libro que publicó: Liber abaci (Libro del ábaco), donde venía el famosísimo problema de los conejos.

Aunque dicha sucesión, ya había salido a la luz mucho antes de que fuera publicada por Fibonacci, concretamente la habían estudiado matemáticos hindúes, tales cómo Gopala y Hemachandra, pero no se hizo famosa hasta que se publicó en el libro Liber abaci.

No es de extrañar que Fibonacci estuviera influenciado por dichos autores, ya que era un estudioso de las matemáticas hindúes.

Pues bien, la serie de Fibonacci, es aquella donde cada número es el resultado de sumar los dos que lo preceden. Así, la primera y más básica serie de Fibonacci sería:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, ...

Que responde a la fórmula:

F_n= F_n-1+ F_n-2

De forma más estricta, matemáticamente hablando, la sucesión de Fibonacci es una progresión numérica tal que para todo n perteneciente a N, suponiendo que la serie empieza en 0, tenemos que:

· F(1) = 0....................; para n = 1 (Suponiendo que es el primer término de la serie)
· F(2) = 1....................; para n = 2 (El segundo término de la serie)
· F(n) = F_n-1+ F_n-2.......; para todo n > 2.

La misión de este capítulo es desarrollar una función, en lenguaje R, que devuelva los parámetros de la serie de Fibonacci. La cantidad de parámetros será el valor de entrada a la función y vendrá determinado por el usuario.

El nombre de la función será: SerieFibonacci y tendrá un parámetro de entrada llamado longitud y devolverá por pantalla de consola, la sucesión de números de Fibonacci de longitud dada por el usuario.

La función en sí, es la siguiente:

#######################################################################
#
# Este archivo es propiedad intelectual del blog Aqueronte,
# cuya dirección web, es la siguiente:
#                                                  
#                   http://unbarquero.blogspot.com/   
#
# Se permite cualquier modificación del archivo siempre y cuando
# se mantenga la autoría del autor.
#
# El autor no se responsabiliza de las consecuencias que pueda
# ocasionar éste código debido a un uso inadecuado del mismo.
#
#######################################################################
#
# Función: SerieFibonacci  Versión:   vs0.0
# Fecha:   14/09/09        R Versión: 2.9.1
#
# Autor:    Manuel Caballero
# Compañía: Hades
#
#######################################################################
#
# Notas: Esta función devuelve la serie de Fibonacci con la
#   longitud que determine el usuario.
#
# Datos de Entrada:
#  · longitud: Dimensión de la serie de Fibonacci a mostrar.
#
# Datos de Salida:
#  · fibonacci: La serie de Fibonacci en cuestión.
#
#######################################################################
SerieFibonacci <- function(longitud)
{
   fibonacci <- 0
   fibonacci[1] <- 0

   if (longitud > 1)
   {
     fibonacci[2] <- 1
   
     if (longitud > 2)
     {
       for (i in 3:longitud)
       {
         fibonacci[i] <- fibonacci[i-2] + fibonacci[i-1]
       }
     }
   }
   fibonacci
} 

Comprobamos que funciona de forma correcta:

> SerieFibonacci(1)
[1] 0
> SerieFibonacci(2)
[1] 0 1
> SerieFibonacci(3)
[1] 0 1 1
> SerieFibonacci(5)
[1] 0 1 1 2 3
> SerieFibonacci(10)
[1] 0 1 1 2 3 5 8 13 21 34

Vemos que nos muestra por consola los números que pertenecen a dicha sucesión dada una longitud como parámetro, ahora, realizaremos una última consulta con un valor grande de longitud:

> SerieFibonacci(60)
[1]............................0.........................1......................1..........................2.........................3
[6]............................5.........................8....................13........................21.......................34
[11]........................55.......................89..................144.....................233.....................377
[16]......................610....................987................1597...................2584...................4181
[21]....................6765................10946..............17711.................28657................46368
[26].................75025..............121393...........196418................317811..............514229
[31]..............832040............1346269.........2178309............3524578............5702887
[36]............9227465..........14930352.......24157817..........39088169.........63245986
[41]........102334155........165580141.....267914296...... 433494437....... 701408733
[46]......1134903170......1836311903..2971215073.....4807526976......7778742049
[51]...12586269025...20365011074..32951280099....53316291173....86267571272
[56] 139583862445 225851433717 365435296162 591286729879 956722026041

Podemos apreciar que funciona de forma correcta.

---

Se puede descargar el script SerieFibonacci.r del siguiente enlace:

		SerieFibonacci.r
		SerieFibonacci.r

---

Profundizaremos un poquito más, que la ocasión lo merece. Analizaremos cómo se puede representar, de forma geométrica, esta serie:

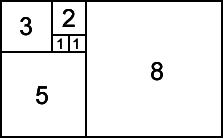
• Comenzamos dibujando un cuadrado de lado 1.

• Apoyado en uno de sus lados, de lado 1, dibujamos otro cuadrado igual. Dispondremos ahora de dos cuadrados de lado 1 respectivamente.
  

• Apoyándonos simultáneamente en estos dos cuadrados, en conjunto hacen 2 lados, dibujamos un cuadrado de lado 2.

• Apoyándonos en este y en uno de los anteriores un cuadrado de lado 3

• etc...

Obtendríamos la siguiente figura:

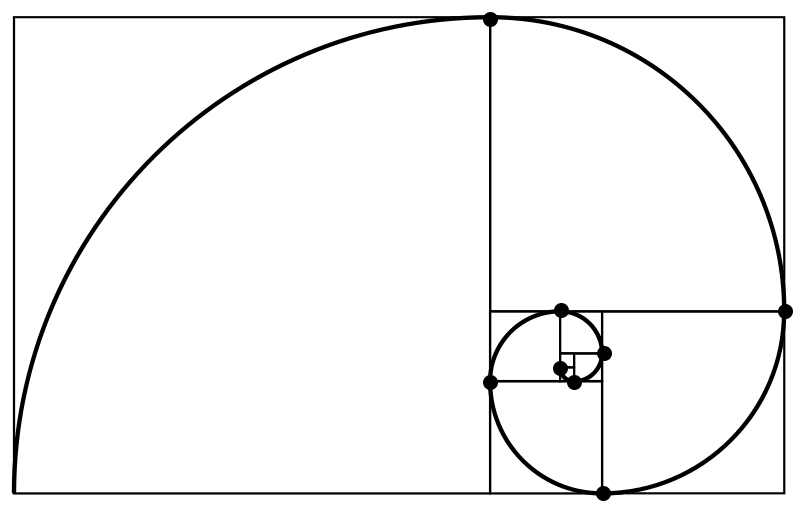
Si ahora, unimos los vértices de los rectángulos que hemos creado, se nos va formando una curva denominada: la espiral de Durero:

Una espiral, que de manera bastante aproximada, está presente en el crecimiento de las conchas de los moluscos, en los cuernos de los rumiantes, etc.

En otras palabras, la espiral del crecimiento y la forma del reino animal y vegetal. Fibonacci sin pretenderlo, había hallado la llave del crecimiento en la Naturaleza.

Pero esta serie no acaba aquí, está presente en el arte, por ejemplo: En las estructuras formales de las sonatas de Mozart, en la Quinta Sinfonía de Beethoven, en obras de Schubert y Debussý.

Las relaciones entre articulaciones en el hombre de Vitruvio y en otras obras de Leonardo da Vinci, como por ejemplo, la armonía en la expresión del cuadro de la Mona Lisa:

También, esta presente, como ya se ha comentado anteriormente, en la naturaleza, en el crecimiento de plantas y hojas de ciertos vegetales y plantas, por ejemplo, en el girasol:

Y por último, pero no menos importante, una de las características de la serie de Fibonacci es que, a medida que n aumenta, la relación entre dos términos sucesivos tiende a Φ, siendo este el valor de la proporción o número áureo.

n	1	2	3	4	5	6	7	8	9
F(n)	1	1	2	3	5	8	13	21	34
F(n)/F(n-1)		1	2	1,5	1,666...	1,6	1,625	1,615...	1,619...

En otras palabras, la serie de Fibonacci es también llamada la serie de Dios porque la relación entre dos términos sucesivos tiende al número áureo.

En fin, es una serie grandiosamente interesante y fácil de estudio, y aunque me dejo cosas en el baúl, espero haber puesto mi granito de arena, en forma de homenaje, a esta expresión matemática.