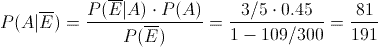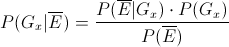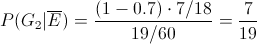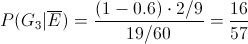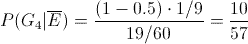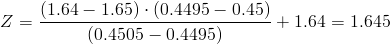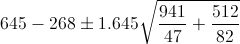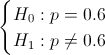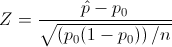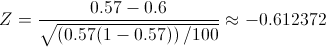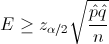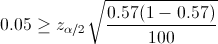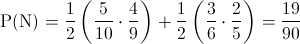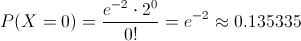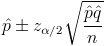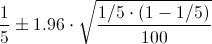Problema34: Análisis de Regresión

Ej34. Los datos reflejados en la siguiente tabla relacionan los niveles de concentración de una sustancia, presentes en 6 muestras, con la respuesta observada en un colorímetro:

x.	4.2450	5.9480	12.8650	26.6660	35.1860	50.6510
y	0.0280	0.0440	0.0680	0.0920	0.1095	0.1295

El objetivo es encontrar una curva de calibración del tipo: y = α·e^βx, que permita determinar la concentración a partir de la respuesta observada en el colorímetro.

Determinar el valor de α y de β.

NOTA: La variable x representa la respuesta del colorímetro y la variable y representa la concentración de la sustancia de la muestra. 

Este problema comparte los mismos datos que el Problema14 pero con distinta curva de calibración.



El modelo que nos ofrece el problema no es un modelo lineal simple, por lo que tenemos que adecuarlo, en este caso, actuamos mediante logaritmo neperiano:

Ln(y) = Ln(α·e^βx) = Ln(α) + β·x

Cambio de Variable:
¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨
· y* = Ln(y)
· b₀ = Ln(α)

El modelo ajustado, con el cambio de variable, es:

y* = b₀ + b₁·x
Y la tabla quedará tal y como sigue:

x*.	4.2450	5.9480	12.8650	26.6660	35.1860	50.6510
y*	Ln(0.0280).	Ln(0.0440).	Ln(0.0680).	Ln(0.0920).	Ln(0.1095)	Ln(0.1295)

Ahora, podemos hacer una recopilación de datos que se extraen de la tabla una vez realizado el cambio de variable.

· n = 6

·

·

·

·

·


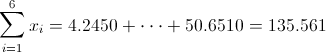
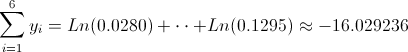
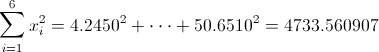
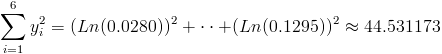
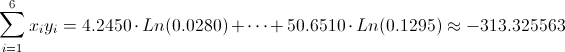
Para calcular la pendiente, la expresión matemática es:

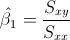
Para obtener su valor, necesitamos saber los valores de Sxy y Sxx:

·

·


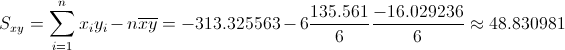
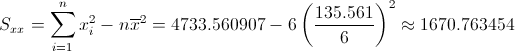
Por lo tanto, la pendiente es:

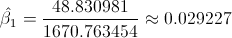
Una vez obtenida la pendiente, podemos tener el valor del estimador para la ordenada. Sustituimos valores:

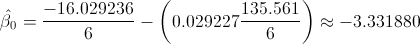
Por lo tanto, la ecuación de regresión ajustada es:

y*(x) = -3.331880 + 0.029227·x

Siendo:

· y* = Ln(y)
· b₀ = Ln(α) = -3.331880
· b₁ = β = 0.029227

El modelo no lineal quedará:

 y = 0.035726·e^0.029227·x

Siendo:

· α = e^-3.331880 ≈ 0.035726

Problema100: Probabilidad

Ej100. Un determinado producto químico puede contener tres sustancias tóxicas, éstas son: A, E y O, que son motivo de sanción por el Ministerio de Medio Ambiente. Por la experiencia, se sabe que de cada 1000 unidades producidas, aproximadamente 15 tienen el elemento A, 17 el E y 21 el C.

Además se sabe que de dichas unidades producidas se obtienen 10 elementos de A y E, 9 de E y O, 7 de A y O, y finalmente, 970 no contienen ninguno de los tres elementos.

Un inspector selecciona una unidad al azar. Obtener:

a) La probabilidad de que la empresa sea sancionada (aparezca alguno de los elementos tóxicos).

b) La probabilidad de que se solo se encuentre el elemento A.

c) La probabilidad de que se detecten solamente, los elementos A y E.

d) La probabilidad de que se detecte más de un elemento.



Recopilamos información del enunciado del problema. Definimos los elementos:

· A ≡ 'Elemento tóxico A'
· E ≡ 'Elemento tóxico E'
· O ≡ 'Elemento tóxico O'

De cada 1000 muestras producidas, la probabilidad de presencia de cada elemento es la siguiente:

· P(A) = 15/1000 = 0.015
· P(E) = 17/1000 = 0.017
· P(O) = 21/1000 = 0.021

· P(A ∩ E) = 10/1000 = 0.01
· P(E ∩ O) = 9/1000 = 0.009
· P(A ∩ O) = 7/1000 = 0.007

· P(Ā ∩ Ē ∩ Ō) = 970/1000 = 0.97

Ya estamos en disposición de obtener las soluciones de los apartados del enunciado de este problema.

Apartado a)

En este apartado nos piden la probabilidad de que la empresa sea sancionada, para ello, debe estar presente al menos, uno de los elementos tóxicos en el producto químico, en otras palabras:

· P(A ∪ E ∪ O) = P(A) + P(E) + P(O) - P(A ∩ E) - P(E ∩ O) - P(A ∩ O) + P(A ∩ E ∩ O)

Para obtener la solución a este apartado, nos falta saber el valor del séptimo elemento en la expresión anterior: P(A ∩ E ∩ O), para obtenerlo, nos vamos a basar en el siguiente elemento conocido:

· P(Ā ∩ Ē ∩ Ō) = P[(1- A) ∩ (1 - E) ∩ (1 - O)]

Operamos:

 · P(Ā ∩ Ē ∩ Ō) = 1 - P(A) - P(E) - P(O) + P(A ∩ E) + P(E ∩ O) + P(A ∩ O) - P(A ∩ E ∩ O)

Al tener todos los datos disponibles, sustituimos el valor que deseamos calcular:

 · P(A ∩ E ∩ O) = 1 - 0.015 - 0.017 - 0.021 + 0.01 + 0.009 + 0.007 - 0.97 = 0.003

Ya estamos en disposición de obtener la solución a este apartado:

· P(A ∪ E ∪ O) = 0.015 + 0.017 + 0.021 - 0.01 - 0.009 - 0.007 + 0.003 = 0.03

Por lo tanto, la probabilidad de que la empresa sea sancionada por el Ministerio de Medio Ambiente es de 0.03.

· NOTA: Otra forma más fácil y rápida de obtener la solución a este apartado es la siguiente:

Sustituimos valores:

· P(A ∪ E ∪ O) = 1 - 0.97 = 0.03

Como se puede comprobar, da el mismo resultado. En el apartado se ha optado por la forma larga (y algo tediosa) para resolverlo ya que el resultado intermedio obtenido nos será de utilidad en los posteriores apartados.


Apartado b)

En este apartado nos piden la probabilidad de que solo aparezca el elemento tóxico A, por lo tanto, tenemos:

· P(A ∩ Ē ∩ Ō) =  P[A ∩ (1 - E) ∩ (1 - O)]

Operamos:

 · P(A ∩ Ē ∩ Ō) = P(A) - P(A ∩ E) - P(A ∩ O) + P(A ∩ E ∩ O)

Sustituimos valores para obtener la solución a este apartado:

 · P(A ∩ Ē ∩ Ō) = 0.015 - 0.01 - 0.007 + 0.003 = 0.001

Por lo tanto, la probabilidad de que solo aparezca el elemento tóxico A en el producto químico es de 0.001.


Apartado c)

En este apartado nos piden la probabilidad de que aparezcan los elementos tóxicos A y E, por lo tanto, tenemos:

· P(A ∩ E ∩ Ō) =  P[A ∩ E ∩ (1 - O)]

Operamos:

 · P(A ∩ E ∩ Ō) = P(A ∩ E) - P(A ∩ E ∩ O)

Sustituimos valores para obtener la solución a este apartado:

 · P(A ∩ E ∩ Ō) = 0.01 - 0.003 = 0.007

Por lo tanto, la probabilidad de que aparezcan los elementos tóxicos A y E en el producto químico es de 0.007.


Apartado d)

En este apartado nos piden la probabilidad de que aparezcan más de un elemento tóxico, por lo tanto, tenemos:

· P[(A ∩ E ∩ Ō) ∪ (A ∩ E ∩ O) ∪ (A ∩ Ē ∩ O) ∪ (Ā ∩ E ∩ O)]

Los elementos 1 y 2 de la expresión anterior ya los tenemos calculados, nos faltan los dos restantes, vamos a obtenerlos:

· [El.3] P(A ∩ Ē ∩ O) = P[A ∩ (1 - E) ∩ O] = P(A ∩ O) - P(A ∩ E ∩ O) = 0.007 - 0.003 = 0.004
· [El.4] P(Ā ∩ E ∩ O) = P[(1 - A) ∩ E ∩ O] = P(E ∩ O) - P(A ∩ E ∩ O) = 0.009 - 0.003 = 0.006

 Ya tenemos todos los datos necesarios para obtener la solución a este apartado, sustituimos valores:

 · P[(A ∩ E ∩ Ō) ∪ (A ∩ E ∩ O) ∪ (A ∩ Ē ∩ O) ∪ (Ā ∩ E ∩ O)] = 0.007 + 0.003 + 0.004 + 0.006 = 0.02

Por lo tanto, la probabilidad de que aparezcan más de un elemento tóxico en el producto químico es de 0.02.

Problema99: Probabilidad

Ej99.Dos profesores de la Universidad de Sevilla comparten una oficina con un solo teléfono. Han comprobado que el 45% de las llamadas recibidas son para el profesor A y el resto para el profesor B.

Dos de cada cinco llamadas que recibe el profesor A son externas y las otras tres, son llamadas realizadas desde la misma Universidad. El profesor B recibe cuatro de cada seis llamadas desde la Universidad y el resto externas.

Obtener:

a) Calcular la probabilidad de que se reciba en la oficina, una llamada externa.

b) Sabiendo que se ha recibido una llamada realizada desde la Universidad en la oficina, ¿qué probabilidad hay de que fuera dirigida al profesor A?.



Recopilamos información del enunciado del problema. Definimos los elementos:

· A ≡ 'Llamadas recibidas por el profesor A'
· B ≡ 'Llamadas recibidas por el profesor B'

La probabilidad de cada elemento es:

· P(A) = 0.45
· P(B) = 1- 0.45 = 0.55

Las llamadas pueden ser de dos tipos, externas o procedentes de la misma Universidad, por lo tanto, definimos el suceso siguiente:

· E ≡ 'Llamadas externas'

El complemento del suceso anterior sería las llamadas procedentes desde la propia Universidad. El enunciado del problema, nos ofrece información de la probabilidad dependiendo de cada profesor y si las llamadas son externas o no:

· P(E|A) = 2/5
· P(Ē|A) = 3/5

· P(Ē|B) = 4/6 = 2/3
· P(E|B) = 1 - 2/3 = 1/3

Ya estamos en disposición de obtener las soluciones de los apartados del enunciado de este problema.


Apartado a)

En este apartado nos piden obtener la probabilidad de que las llamadas sean externas, éste término es fácil de obtener mediante la Probabilidad Total:

· P(E) = P(E|A)·P(A) + P(E|B)·P(B) = (2/5)·0.45 + (1/3)·0.55 = 109/300

Por lo tanto, la probabilidad de que la oficina que comparten ambos profesores, las llamadas sean externas es de, aproximadamente 0.363333.


Apartado b)

En este apartado nos piden obtener la probabilidad de que sabiendo que se recibe una llamada desde la propia Universidad, ésta sea para el profesor A.

Para obtener dicha probabilidad debemos emplear el Teorema de Bayes:

Por lo tanto, la probabilidad de que siendo una llamada desde la propia Universidad ésta sea para el profesor A es de, aproximadamente 0.424084.

Problema98: Probabilidad

Ej98. Consideremos a 18 tiradores clasificados en 4 grupos. En el primer grupo hay 5 tiradores con probabilidades 0.8 de dar en el blanco, en el segundo hay 7 con probabilidad 0.7, en el tercero hay 4 con probabilidad de 0.6 y en el ultimo 2 con probabilidad 0.5 de dar en el blanco.

Se selecciona aleatoriamente un tirador, dispara y no da en el blanco. ¿A qué grupo es más probable que pertenezca?.



Recopilamos información del enunciado del problema. Definimos los elementos:

· G_x ≡ 'Tirador del Grupo x'
· E ≡ 'Dar en el blanco'

Existen cuatro grupos de tiradores:

· G₁ ≡ 'Tirador del Grupo 1'. En este grupo hay 5 tiradores.
· G₂ ≡ 'Tirador del Grupo 2'. En este grupo hay 7 tiradores.
· G₃ ≡ 'Tirador del Grupo 3'. En este grupo hay 4 tiradores.
· G₄ ≡ 'Tirador del Grupo 4'. En este grupo hay 2 tiradores.

Por lo tanto, existen, en total, 5 + 7 + 4 + 2 = 18 tiradores.

La probabilidad de escoger a un tirador de su grupo correspondiente es la siguiente:

· P(G₁) = 5/18
· P(G₂) = 7/18
· P(G₃) = 4/18 = 2/9
· P(G₄) = 2/18 = 1/9

El enunciado nos ofrece información de la probabilidad de dar en el blanco dependiendo del grupo de tiradores escogido:

· P(E|G₁) = 0.8
· P(E|G₂) = 0.7
· P(E|G₃) = 0.6
· P(E|G₄) = 0.5

Y lo que nos pide el enunciado del problema es,dado que se ha escogido un tirador al azar y éste no haya dado en el blanco, ¿a qué grupo es más probable que pertenezca?. Dicho estudio debemos realizarlo para cada grupo de la siguiente manera:

 

En dicha expresión, hay dos elementos que vamos a manipularlos y obtenerlos antes de abordar el problema, éstos son los siguientes:

· P(Ē) y P(Ē|G_x)

Empezamos por el primero que consiste en la probabilidad de no dar en el blanco, éste término es fácil de obtener mediante la Probabilidad Total, pero previamente, vamos a obtener su complementario, la probabilidad de dar en el blanco:

· P(E) = P(E|G₁)·P(G₁) + P(E|G₂)·P(G₂) + P(E|G₃)·P(G₃) + P(E|G₄)·P(G₄)

Sustituimos valores:

 · P(E) = 0.8·(5/18) + 0.7·(7/18) + 0.6·(2/9) + 0.5·(1/9) = 41/60

Por lo tanto, la probabilidad de no dar al blanco es su complementario:

 · P(Ē) = 1 - P(E) = 1 - 41/60 = 19/60

Una vez obtenido el primer elemento que es necesario para dar respuesta a este problema, vamos a por el segundo. En este caso, vamos a manipular la expresión:

Por lo tato, la expresión queda de la siguiente manera:

· P(Ē|G_x) = 1 - P(E|G_x)

En estos momentos, estamos en disposición de abordar lo que nos piden en el enunciado del problema, para ello, analizamos cada grupo.

· Grupo 1.

Por lo tanto, la probabilidad de que dado que no se ha dado en el blanco, el tirador escogido al azar sea del grupo 1, es de, aproximadamente 0.175439.

· Grupo 2.

Por lo tanto, la probabilidad de que dado que no se ha dado en el blanco, el tirador escogido al azar sea del grupo 2, es de, aproximadamente 0.368421.

· Grupo 3.

Por lo tanto, la probabilidad de que dado que no se ha dado en el blanco, el tirador escogido al azar sea del grupo 3, es de, aproximadamente 0.280702.

· Grupo 4.

Por lo tanto, la probabilidad de que dado que no se ha dado en el blanco, el tirador escogido al azar sea del grupo 4, es de, aproximadamente 0.175439.


Por lo tanto, el grupo más probable al que pertenezca el tirador, dadas las condiciones expuestas en el enunciado del problema, es el Grupo 2.

Problema97: Probabilidad

Ej97. Una compañía de desarrollo urbano está considerando la posibilidad de construir un centro comercial llamado Luz Shopping en un sector de Jerez de la Frontera. Un elemento vital en esta consideración, es un proyecto de una autovía que une este sector con el acceso a la ciudad.

Si el consejo municipal aprueba esta autovía, hay una probabilidad de 0.90 de que la compañía construya el centro comercial, en tanto que, si la autovía no es aprobada, la probabilidad es solo 0.20.

Basándose en la información disponible, el presidente de la compañía estima que hay una probabilidad de 0.60 que la autovía sea aprobada.

Obtener:

a) ¿Cuál es la probabilidad que la compañía construya el centro comercial?

b) Dado que el centro comercial fue construido. ¿Cuál es la probabilidad de que la autovía haya sido aprobada?


Recopilamos información del enunciado del problema definiendo los siguientes sucesos:

· E ≡ 'Se construye el edificio'.
· O ≡ 'Se aprueba la autovía'.

· P(O) = 0.6.

· P(E|O) = 0.9.
· P(E|Ō) = 0.2.

Ya estamos en disposición de resolver los distintos apartados que nos ofrece el enunciado del problema.


Apartado a)

En este apartado nos piden obtener la probabilidad de que la compañía construya el centro comercial, para ello, debemos emplear el teorema de la Probabilidad Total:

P(E) = P(E|O)·P(O) + P(E|Ō)·P(Ō) = 0.9·0.6 + 0.2·(1 - 0.6) = 31/50

Por lo tanto, la probabilidad de que la compañía construya el centro comercial es de 0.62.


Apartado b)

En esta ocasión, debemos obtener la probabilidad de dado de que se construye el edificio comercial, se haya aprobado el proyecto de la autovía, para resolver este apartado, emplearemos la Ley de Bayes:

Sustituimos valores para obtener la solución:

Por lo tanto, la probabilidad de dado de que se construye el edificio comercial, se haya aprobado el proyecto de la autovía es de, aproximadamente, 0.870968.

Problema96: Probabilidad

Ej96. Una urna contiene 5 bolas blancas y 6 negras, se extrae al azar sucesivamente dos bolas. 

Obtener, teniendo en cuenta que no se reponen las bolas extraídas, los siguientes apartados:

a) La probabilidad que las dos resulten blancas.

b) La probabilidad de obtener una bola de cada color.



Teniendo en cuenta que se reponen las bolas extraídas, obtener los siguientes apartados:

c) La probabilidad que las dos resulten blancas.

d) La probabilidad de obtener una bola de cada color.

Recopilamos información del enunciado del problema.

Tenemos una urna que contiene las siguientes bolas:

· 5 Bolas blancas.
· 6 Bolas negras.

En total, en la urna hay: 5 + 6 = 11 bolas.

Definimos los elementos:

· B ≡ 'La bola es blanca'
· N ≡ 'La bola es negra'

La probabilidad de cada elemento se muestra a continuación:

· P(B) = 5/11
· P(N) = 6/11

En estos momentos estamos en disposición de resolver los distintos apartados que nos ofrece el enunciado del problema.

Apartado a)

En este apartado, debemos tener en cuenta que las bolas extraídas de la urna no se reponen, esto quiere decir, que cada vez que saquemos una bola de la urna, el total de bolas resultantes en dicha urna, se reducirá en una unidad.

La probabilidad que debemos obtener es la siguiente (ambas bolas extraídas sean blancas):

· P(B ∩ B) = (5/11)·(4/10) = 2/11

Por lo tanto, la probabilidad de sacar dos bolas blancas de la urna dada sin reposición es de, aproximadamente 0.181818.

Apartado b)

En este apartado, debemos tener en cuenta que las bolas extraídas de la urna no se reponen, esto quiere decir, que cada vez que saquemos una bola de la urna, el total de bolas resultantes en dicha urna, se reducirá en una unidad.

La probabilidad que debemos obtener es la siguiente (ambas bolas extraídas sean de diferente color):

· P[(B ∩ N) ∪ (N ∩ B)] = (5/11)·(6/10) +  (6/11)·(5/10) = 6/11

Por lo tanto, la probabilidad de sacar dos bolas de diferente color de la urna dada sin reposición es de, aproximadamente 0.545455.

Apartado c)

En este apartado, debemos tener en cuenta que las bolas extraídas de la urna se reponen, esto quiere decir, que cada vez que saquemos una bola de la urna, se volverá a introducir después de ver de que color es, en otras palabras, la urna siempre tiene el número total de bolas.

La probabilidad que debemos obtener es la siguiente (ambas bolas extraídas sean blancas):

· P(B ∩ B) = (5/11)·(5/11) = 25/121

Por lo tanto, la probabilidad de sacar dos bolas blancas de la urna dada con reposición es de, aproximadamente 0.206612.


Apartado d)

En este apartado, debemos tener en cuenta que las bolas extraídas de la urna se reponen, esto quiere decir, que cada vez que saquemos una bola de la urna, se volverá a introducir después de ver de que color es, en otras palabras, la urna siempre tiene el número total de bolas.

La probabilidad que debemos obtener es la siguiente (ambas bolas extraídas sean de diferente color):

· P[(B ∩ N) ∪ (N ∩ B)] = (5/11)·(6/11) +  (6/11)·(5/11) = 60/121

Por lo tanto, la probabilidad de sacar dos bolas de diferente color de la urna dada con reposición es de, aproximadamente 0.495868.

Problema95: Probabilidad

Ej95. De un grupo de personas, el 30% practica fútbol y el 40% juega ajedrez. De los futbolistas, el 50% juega ajedrez.

Si se selecciona aleatoriamente una persona, obtener:

a) La probabilidad que juegue fútbol o ajedrez.

b) La probabilidad que practique solo uno de estos deportes.

c) La probabilidad que no practique ni fútbol ni ajedrez.


Realizamos una recopilación de datos dados por el enunciado del problema:

· E ≡ 'Juega al fútbol'.
· O ≡ 'Juega al ajedrez'.

· P(E) = 0.3.
· P(O) = 0.4.
· P(O|E) = 0.5.

Pasamos a resolver los apartados que nos propone el enunciado del problema.


Apartado a)

En este apartado nos piden obtener la probabilidad de que al escoger un individuo al azar, éste juegue al fútbol o al ajedrez:

P(E ∪ O) = P(E) + P(O) - P(E ∩ O)

Donde (mediante la regla de la multiplicación):

· P(E ∩ O) = P(O|E)·P(E)

Sustituimos para obtener la solución a este apartado:

P(E ∪ O) = P(E) + P(O) - P(E ∩ O) = P(E) + P(O) - P(O|E)·P(E) = 0.3 + 0.4 - 0.5·0.3 = 0.55

Por lo tanto, la probabilidad de que el individuo juegue al fútbol o al ajedrez es de 0.55.


Apartado b)

En este apartado nos piden que obtengamos la probabilidad de que al seleccionar, al azar, un individuo éste, solo juegue al fútbol o al ajedrez:

· P[(E ∩ Ō) ∪ (Ē ∩ O)]

Manipulamos la expresión anterior:

· P[(E ∩ Ō) ∪ (Ē ∩ O)] = P(E ∩ Ō) + P(Ē ∩ O) - P[(E ∩ Ō) ∩ (Ē ∩ O)] = P(E ∩ Ō) + P(Ē ∩ O) - P[(E ∩ (1 - O)) ∩ ((1 - E) ∩ O)]

Por el momento, nos vamos a centrar en el tercer miembro. Simplificamos:

· P[(E ∩ Ō) ∪ (Ē ∩ O)] = P(E ∩ Ō) + P(Ē ∩ O) - P[(E - (E ∩ O)) ∩ (O - (E ∩ O))]

Operamos:

· P[(E ∩ Ō) ∪ (Ē ∩ O)] = P(E ∩ Ō) + P(Ē ∩ O) + P(E ∩ O) - P(E ∩ O) - P(E ∩ O) + P(E ∩ O)

Volvemos a simplificar:

· P[(E ∩ Ō) ∪ (Ē ∩ O)] = P(E ∩ Ō) + P(Ē ∩ O)

Llegados a este punto, vamos a manipular la expresión resultante:

· P[(E ∩ Ō) ∪ (Ē ∩ O)] = P[E ∩ (1 - O)] + P[(1 - E) ∩ O] = P(E) - P(E ∩ O) + P(O) - P(E ∩ O)

Simplificamos:

· P[(E ∩ Ō) ∪ (Ē ∩ O)] = P(E) + P(O) - 2·P(E ∩ O) = P(E) + P(O) - 2·P(O|E)·P(E)

Y por fin, sustituimos valores para obtener la solución a este apartado:

· P[(E ∩ Ō) ∪ (Ē ∩ O)] = P(E) + P(O) - 2·P(O|E)·P(E) = 0.3 + 0.4 - 2·0.5·0.3 = 0.4

Por lo tanto, la probabilidad de que el individuo juegue solo al fútbol o solo al ajedrez es de 0.4.


Apartado c)

En este apartado nos piden obtener la probabilidad de que el individuo escogido, no juegue ni al fútbol ni al ajedrez:

· P(Ē ∪ Ō) = 1 - P(E ∪ O)

Nos apoyamos en el resultado obtenido en el primer apartado para obtener la solución a este apartado:

· P(Ē ∪ Ō) = 1 - P(E ∪ O) = 1 - 0.55 = 0.45

Por lo tanto, la probabilidad de que dado que el individuo escogido al azar, no juegue ni al fútbol ni al ajedrez es de 0.45.

Problema94: Probabilidad

Ej94. Dos personas A y B, se distribuyen aleatoriamente en tres oficinas numeradas de la siguiente manera: 1, 2 y 3.

Pudiendo estar ambas personas en una misma oficina, obtener:

a) La probabilidad de que la oficina 2 se quede vacía.

b) La probabilidad de que dos oficinas se queden vacías.

En este problema, tenemos dos personas y tres oficinas, la nomenclatura que emplearemos será la siguiente:


· A_XB_Y ≡ Indicará que la persona A está en la oficina que indica el subíndice X y la persona B estará en la oficina que indica el subíndice Y.

La clave de este problema es obtener el espacio muestral:

Ω = {A₁B₁, A₁B₂, A₁B₃, A₂B₁, A₂B₂, A₂B₃, A₃B₁, A₃B₂, A₃B₃}

Hacen un total de 9 maneras diferentes de que ambas personas estén repartidas entre las 3 oficinas.

En estos momentos, estamos listos para resolver los apartados dados por el enunciado del problema.


Apartado a)

Hay que obtener la probabilidad de que la oficina 2 se quede vacía. Definimos el suceso:

· X ≡ 'La oficina 2 se quede vacía'.

El número de elementos, en el espacio muestral, dónde ninguna de las dos personas están en la oficina 2 es de 4.

Por lo tanto, la solución a este apartado es la siguiente:

· P(X) = 4/9

Existe una probabilidad de, aproximadamente 0.444444 de que ambas personas no estén en la oficina 2.

Apartado b)

Hay que obtener la probabilidad de que dos oficinas se queden vacías, dicho de otra manera, de que ambas personas estén en la misma oficina. Definimos el suceso:

· M ≡ 'Dos oficinas se queden vacías'.

El número de elementos, en el espacio muestral, dónde ambas personas estén en la misma oficina es de 3.

Por lo tanto, la solución a este apartado es la siguiente:


· P(M) = 3/9 = 1/3

Existe una probabilidad de, aproximadamente 0.333333 de que dos oficinas se queden vacías.

Problema93: Probabilidad

Ej93. Ante el inminente arranque de la competición de fútbol europeo: Eurocopa Polonia/Ucrania 2012, se quiere realizar un estudio estadístico sobre los equipos que van a participar.

Se sabe, que la configuración para ser campeón de la competición sigue el siguiente patrón:

· 1º: Ser primero o segundo de grupo.
· 2º: Pasar cuartos de final.
· 3º: Pasar semifinales.
· 4º: Ganar la final.

Dicho patrón se ha mantenido desde la Eurocopa Inglaterra 1996, por lo tanto, los datos obtenidos desde ésa competición hasta la última (Eurocopa Austria/Suiza 2008) son:

Equipos/Grupos		1º Grupo	2º Grupo		1/4 Final	Semifinales	Final
· Grupo A
Polonia
Grecia			1		1	1	1
Rusia			1		1
Rep. Checa		1	1		2	1
· Grupo B
Holanda		2	2		2
Dinamarca			1
Alemania		1	1		2	2	1
Portugal		4			2	1
· Grupo C
España		2	1		1	1	1
Italia		1	1		1	1
Irlanda
Croacia		1	1
· Grupo D
Francia		2	1		2	1	1
Inglaterra		1	1		1
Ucrania
Suecia		1

· NOTA: Los datos mostrados en la anterior tabla corresponde a las veces que los equipos han conseguido superar las fases indicadas. El computo de datos corresponde a las 4 últimas Eurocopas. Los equipos que no tienen datos es que no han conseguido superar la fase o no han llegado a disputarla.

Se desea saber:

a) ¿Qué equipos tienen más probabilidades de pasar la fase de grupos? En otras palabras, ¿qué equipos son más probables que lleguen a cuartos de final?.

b) Teniendo en cuenta los datos anteriores, ¿qué equipos tienen más probabilidades de pasar los cuartos de final? En otras palabras, ¿que equipos son más probables que lleguen a semifinales?.

c) Teniendo en cuenta los datos anteriores, ¿qué equipos tienen más probabilidades de pasar la semifinal? En otras palabras, ¿qué equipos son más probables que lleguen a la final?.

d) Teniendo en cuenta los datos anteriores, ¿qué equipos tienen más probabilidades de ganar la Eurocopa Polonia/Ucrania 2012?.

e) Sin tener en cuenta ningún análisis previo, simplemente con los datos expuestos, ¿cuáles equipos tienen más probabilidad de ganar la Eurocopa Polonia/Ucrania 2012?.


Apartado a)

En este apartado nos piden la probabilidad de pasar la 1ª Fase de Grupo, para ello, el equipo debe quedar primero o segundo del grupo en el que juegue:

· P(Pasar 1ª Fase Grupo) = P(Ser 1º Grupo ∪ Ser 2º Grupo)

Lo realizamos para todos los equipos:

· P(Polonia) = 0/4 + 0/4 = 0
· P(Grecia) = 0/4 + 1/4 = 1/4
· P(Rusia) = 0/4 + 1/4 = 1/4
· P(Rep. Checa) = 1/4 + 1/4 = 2/4 = 1/2
· P(Holanda) = 2/4 + 2/4 = 4/4 = 1
· P(Dinamarca) = 0/4 + 1/4 = 1/4
· P(Alemania) = 1/4 + 1/4 = 2/4 = 1/2
· P(Portugal) = 4/4 + 0/4 = 1
· P(España) = 2/4 + 1/4 = 3/4
· P(Italia) = 1/4 + 1/4 = 2/4 = 1/2
· P(Irlanda) = 0/4 + 0/4 = 0
· P(Croacia) = 1/4 + 1/4 = 2/4 = 1/2
· P(Francia) = 2/4 + 1/4 = 3/4
· P(Inglaterra) = 1/4 + 1/4 = 2/4 = 1/2
· P(Ucrania) = 0/4 + 0/4 = 0
· P(Suecia) = 1/4 + 0/4 = 1/4

Con lo datos anteriores, podemos decir que:

· Los equipos que pasarán la primera fase son dos (hasta ahora, siempre han pasado esta primera fase): Portugal y Holanda.
· Los equipos con una alta probabilidad (3/4) de pasar son: España y Francia.
· Los equipos con una probabilidad de 1/2 de pasar son: Rep. Checa, Alemania, Italia, Croacia e Inglaterra.
· Los equipos con una probabilidad de 1/4 de pasar son: Grecia, Rusia, Dinamarca y Suecia.
· Los equipos que no son probables (0) de pasar son: Polonia, Irlanda y Ucrania.

Por lo tanto, por grupos podemos decir que los equipos que pasaran, a cuartos de final, son:

· Grupo A: Rep. Checa, Grecia o Rusia.
· Grupo B: Holanda y Portugal.
· Grupo C: España, Italia o Croacia.
· Grupo D: Francia e Inglaterra.


Apartado b)

Teniendo los equipos que pasarán la 1ª Fase para llegar a ser campeón de la Eurocopa, nos piden cuales de ellos, pasarán a cuartos de final. Para ello, necesitaremos saber cómo están emparejados estos equipos.

La forma es del siguiente tipo:

· 1º Encuentro 1/4 Final: A₁ - B₂
· 2º Encuentro 1/4 Final: B₁ - A₂
· 3º Encuentro 1/4 Final: C₁ - D₂
· 4º Encuentro 1/4 Final: D₁ - C₂

Donde:

· A₁ ≡ Equipo primero del Grupo A.
· A₂ ≡ Equipo segundo del Grupo A.
· B₁ ≡ Equipo primero del Grupo B.
· B₂ ≡ Equipo segundo del Grupo B.
· C₁ ≡ Equipo primero del Grupo C.
· C₂ ≡ Equipo segundo del Grupo C.
· D₁ ≡ Equipo primero del Grupo D.
· D₂ ≡ Equipo segundo del Grupo D.

Con los datos obtenidos del apartado anterior, vamos a analizar, la probabilidad de quedar primero o segundo de grupo.

· Grupo A:

· Probabilidad de ser primero de grupo:

· P(Rep. Checa) = 1/4
· P(Grecia) = 0/4 = 0
· P(Rusia) = 0/4 = 0

· Probabilidad de ser segundo de grupo:

· P(Rep. Checa) = 1/4
· P(Grecia) = 1/4
· P(Rusia) = 1/4

Por lo tanto, para el grupo A:

· A₁ ≡ Rep. Checa.
· A₂ ≡ Rusia o Grecia.

· Grupo B:

· Probabilidad de ser primero de grupo:

· P(Holanda) = 2/4 = 1/2
· P(Portugal) = 4/4 = 1

· Probabilidad de ser segundo de grupo:

· P(Holanda) = 2/4 = 1/2
· P(Portugal) = 0/4 = 0

Por lo tanto, para el grupo B:

· B₁ ≡ Portugal.
· B₂ ≡ Holanda.

· Grupo C:

· Probabilidad de ser primero de grupo:

· P(España) = 2/4 = 1/2
· P(Italia) = 1/4
· P(Croacia) = 1/4

· Probabilidad de ser segundo de grupo:

· P(España) = 1/4
· P(Italia) = 1/4
· P(Croacia) = 1/4

Por lo tanto, para el grupo C:

· C₁ ≡ España.
· C₂ ≡ Italia o Croacia.

· Grupo D:

· Probabilidad de ser primero de grupo:

· P(Francia) = 2/4 = 1/2
· P(Inglaterra) = 1/4

· Probabilidad de ser segundo de grupo:

· P(Francia) = 1/4
· P(Inglaterra) = 1/4

Por lo tanto, para el grupo D:

· D₁ ≡ Francia.
· D₂ ≡ Inglaterra.

Una vez, dispuesto las posiciones de los equipos dependiendo de la probabilidad de quedar primero o segundo de grupo, tenemos los siguientes emparejamientos para disputar los cuartos de final:

· Opción 1:

· 1º Encuentro 1/4 Final: Rep. Checa - Holanda
· 2º Encuentro 1/4 Final: Portugal - Rusia
· 3º Encuentro 1/4 Final: España - Inglaterra
· 4º Encuentro 1/4 Final: Francia - Italia

· Opción 2:

· 1º Encuentro 1/4 Final: Rep. Checa - Holanda
· 2º Encuentro 1/4 Final: Portugal - Grecia
· 3º Encuentro 1/4 Final: España - Inglaterra
· 4º Encuentro 1/4 Final: Francia - Italia

· Opción 3:

· 1º Encuentro 1/4 Final: Rep. Checa - Holanda
· 2º Encuentro 1/4 Final: Portugal - Rusia
· 3º Encuentro 1/4 Final: España - Inglaterra
· 4º Encuentro 1/4 Final: Francia - Croacia

· Opción 4:

· 1º Encuentro 1/4 Final: Rep. Checa - Holanda
· 2º Encuentro 1/4 Final: Portugal - Grecia
· 3º Encuentro 1/4 Final: España - Inglaterra
· 4º Encuentro 1/4 Final: Francia - Croacia

Una vez tenemos las opciones de emparejamientos de partidos, analizamos la probabilidad de pasar los cuartos de final con los datos de la tabla que nos ofrece el enunciado del problema:

· P(Rep. Checa) = 2/4 = 1/2
· P(Rusia) = 1/4
· P(Grecia) = 1/4
· P(Portugal) = 2/4 = 1/2
· P(Holanda) = 2/4 = 1/2
· P(España) = 1/4
· P(Italia) = 1/4
· P(Croacia) = 0/4 = 0
· P(Francia) = 2/4 = 1/2
· P(Inglaterra) = 1/4

Por lo tanto, los equipos que pasarán a semifinales de la Eurocopa Polonia/Ucrania 2012, según las opciones obtenidas anteriormente, son:

· Opción 1:

· 1º Ganador Encuentro 1/4 Final: Rep. Checa u Holanda
· 2º Ganador Encuentro 1/4 Final: Portugal
· 3º Ganador Encuentro 1/4 Final: España o Inglaterra
· 4º Ganador Encuentro 1/4 Final: Francia

· Opción 2:

· 1º Ganador Encuentro 1/4 Final: Rep. Checa u Holanda
· 2º Ganador Encuentro 1/4 Final: Portugal
· 3º Ganador Encuentro 1/4 Final: España o Inglaterra
· 4º Ganador Encuentro 1/4 Final: Francia

· Opción 3:

· 1º Ganador Encuentro 1/4 Final: Rep. Checa u Holanda
· 2º Ganador Encuentro 1/4 Final: Portugal
· 3º Ganador Encuentro 1/4 Final: España o Inglaterra
· 4º Ganador Encuentro 1/4 Final: Francia

· Opción 4:

· 1º Ganador Encuentro 1/4 Final: Rep. Checa u Holanda
· 2º Ganador Encuentro 1/4 Final: Portugal
· 3º Ganador Encuentro 1/4 Final: España o Inglaterra
· 4º Ganador Encuentro 1/4 Final: Francia

Bueno, como se puede ver, todas las opciones desembocan en una sola opción:

· 1º Ganador Encuentro 1/4 Final: Rep. Checa u Holanda
· 2º Ganador Encuentro 1/4 Final: Portugal
· 3º Ganador Encuentro 1/4 Final: España o Inglaterra
· 4º Ganador Encuentro 1/4 Final: Francia


Apartado c)

En este apartado nos piden obtener los equipos que pasarán a la gran final de la Eurocopa Polonia/Ucrania 2012. Para ello, necesitaremos saber cómo están emparejados estos equipos.

La forma es del siguiente tipo:

· 1ª Semifinal: 1º - 3º
· 2ª Semifinal: 2º - 4º

Volvemos a tener varias opciones de emparejamientos, éstas son las siguientes:

· Opción 1:

· 1ª Semifinal: Rep. Checa - España
· 2ª Semifinal: Portugal - Francia

· Opción 2:

· 1ª Semifinal: Rep. Checa - Inglaterra
· 2ª Semifinal: Portugal - Francia

· Opción 3:

· 1ª Semifinal: Holanda - España
· 2ª Semifinal: Portugal - Francia

· Opción 4:

· 1ª Semifinal: Holanda - Inglaterra
· 2ª Semifinal: Portugal - Francia

Una vez tenemos las opciones de emparejamientos de partidos, analizamos la probabilidad de pasar las semifinales, con los datos de la tabla que nos ofrece el enunciado del problema:

· P(Rep. Checa) = 1/4
· P(Holanda) = 0/4 = 0
· P(Portugal) = 1/4
· P(España) = 1/4
· P(Inglaterra) = 0/4 = 0
· P(Francia) = 1/4

Por lo tanto, los equipos que pasarán a la gran final de la Eurocopa Polonia/Ucrania 2012, según las opciones obtenidas anteriormente, son:

· Opción 1:

· 1º Semifinalista: Rep. Checa o España
· 2º Semifinalista: Portugal o Francia

· Opción 2:

· 1º Semifinalista: Rep. Checa
· 2º Semifinalista: Portugal o Francia

· Opción 3:

· 1º Semifinalista: España
· 2º Semifinalista: Portugal o Francia

· Opción 4:

· 1º Semifinalista: Holanda o Inglaterra
· 2º Semifinalista: Portugal o Francia


Apartado d)

Por fin, llegamos al apartado importante, ¿quién ganará la Eurocopa Polonia/Ucrania 2012?. Teniendo en cuenta los datos obtenidos en los anteriores apartados, vamos a intentar dar una respuesta a esta pregunta.

La final, la juegan los equipos ganadores de sus respectivas semifinales, como hemos tenido varias alternativas de estas semifinales vamos a ver cuántas finales obtenemos:

· Opción 1 (4 posibles finales):

· Posible Final: Rep. Checa - Portugal
· Posible Final: Rep. Checa - Francia

· Posible Final: España - Portugal
· Posible Final: España - Francia

· Opción 2 (2 posibles finales):

· Posible Final: Rep. Checa - Portugal
· Posible Final: Rep. Checa - Francia

· Opción 3 (2 posibles finales):

· Posible Final: España - Portugal
· Posible Final: España - Francia

· Opción 4 (4 posibles finales):

· Posible Final: Holanda - Portugal
· Posible Final: Holanda - Francia

· Posible Final: Inglaterra - Portugal
· Posible Final: Inglaterra - Francia

Una vez tenemos las opciones de emparejamientos de partidos, analizamos la probabilidad de ganar la final, con los datos de la tabla que nos ofrece el enunciado del problema:

· P(Rep. Checa) = 0/4 = 0
· P(Holanda) = 0/4 = 0
· P(Portugal) = 0/4 = 0
· P(España) = 1/4
· P(Inglaterra) = 0/4 = 0
· P(Francia) = 1/4

Por lo tanto, el equipo ganador Eurocopa Polonia/Ucrania 2012, según las opciones obtenidas anteriormente, es:

· Opción 1 (4 posibles finales):

· Posible Ganador: Rep. Checa o Portugal
· Posible Ganador: Francia
· Posible Ganador: España
· Posible Ganador: España o Francia

· Opción 2 (2 posibles finales):

· Posible Ganador: Rep. Checa o Portugal
· Posible Ganador: Francia

· Opción 3 (2 posibles finales):

· Posible Ganador: España
· Posible Ganador: España o Francia

· Opción 4 (4 posibles finales):

· Posible Ganador: Holanda o Portugal
· Posible Ganador: Francia
· Posible Ganador: Inglaterra o Portugal
· Posible Ganador: Francia

De los posibles ganadores (18 ganadores), vamos a analizar qué equipo tiene más probabilidad de ganar la Eurocopa Polonia/Ucrania 2012 de cada equipo es:

· P(Rep. Checa) = 2/18 = 1/9
· P(Holanda) = 1/18
· P(Portugal) = 4/18 = 2/9
· P(España) = 4/18 = 2/9
· P(Inglaterra) = 1/18
· P(Francia) = 6/18 = 1/3

Por lo tanto, podemos decir que:

· Equipo más probable que gane la Eurocopa Polonia/Ucrania 2012: Francia.
· Siguientes equipos con probabilidad de ganarla: España o Portugal.
· Después tenemos: Rep. Checa.
· Y por último, los equipos menos probables son: Holanda e Inglaterra.

Bueno, esto es simplemente un estudio estadístico teniendo solo en cuenta sus datos históricos desde la Eurocopa del 1996 hasta la del 2008.

Apartado e)

En este apartado no vamos a analizar las diferentes fases y emparejamientos que pueden darse entre equipos dados sus resultados históricos, simplemente, obtendremos la probabilidad de ganar la Eurocopa Polonia/Ucrania 2012 sabiendo que para ganarla, un equipo debe pasar por las siguientes fases:

· P(Ganar Eurocopa) = P[(Quedar 1º o 2º su Grupo) ∩ (Pasar 1/4 Final) ∩ (Pasar 1/2 Finales) ∩ (Ganar Final)]

Por lo tanto, para cada equipo:

· P(Polonia) = (0/4 + 0/4)·(0/4)·(0/4)·(0/4) = 0
· P(Grecia) = (0/4 + 1/4)·(1/4)·(1/4)·(1/4) = 1/256
· P(Rusia) = (0/4 + 1/4)·(1/4)·(0/4)·(0/4) = 0
· P(Rep. Checa) = (1/4 + 1/4)·(2/4)·(1/4)·(0/4) = 0
· P(Holanda) = (2/4 + 2/4)·(2/4)·(0/4)·(0/4) = 0
· P(Dinamarca) = (0/4 + 1/4)·(0/4)·(0/4)·(0/4) = 0
· P(Alemania) = (1/4 + 1/4)·(2/4)·(2/4)·(1/4) = 1/32
· P(Portugal) = (4/4 + 0/4)·(2/4)·(1/4)·(0/4) = 0
· P(España) = (2/4 + 1/4)·(1/4)·(1/4)·(1/4) = 3/256
· P(Italia) = (1/4 + 1/4)·(1/4)·(1/4)·(0/4) = 0
· P(Irlanda) = (0/4 + 0/4)·(0/4)·(0/4)·(0/4) = 0
· P(Croacia) = (1/4 + 1/4)·(0/4)·(0/4)·(0/4) = 0
· P(Francia) = (2/4 + 1/4)·(2/4)·(1/4)·(1/4) = 3/128
· P(Inglaterra) = (1/4 + 1/4)·(1/4)·(0/4)·(0/4) = 0
· P(Ucrania) = (0/4 + 0/4)·(0/4)·(0/4)·(0/4) = 0
· P(Suecia) = (1/4 + 0/4)·(0/4)·(0/4)·(0/4) = 0

Por lo tanto:

· El equipo con más probabilidad de ganar la Eurocopa Polonia/Ucrania 2012: Alemania.
· Seguido de: Francia.
· Seguido de: España.
· Y por último: Grecia.

¿Y qué hacemos con los datos obtenidos en los otros apartados? Pues vamos a analizarlos de manera breve:

· Podemos ver claramente que, la selección Alemana, las veces que ha pasado la Fase de Grupo, siempre ha jugado la final, ganando una Eurocopa. El problema es que esta Eurocopa, está emparejada con Portugal y Holanda, ambas selecciones siempre han pasado la Fase de Grupos.

De ahí, que difiera los datos obtenidos en los apartados anteriores con éstos.

---

Creo que no hace falta decir, que esto simplemente pretende ser, un ejercicio estadístico. Cualquier parecido con la realidad, es puro azar ;)

Problema84: Estimación y Pruebas de Hipótesis

Ej84. Se necesita una estimación del tiempo de espera en las atracciones de un parque temático ya que existe una preocupación con respecto a una posible bancarrota de la empresa sino se agilizan las colas.
El numero de personas que esperan mas de 20 minutos para entrar a cada atracción, registrado durante 47 días en julio y agosto, tuvo, respectivamente, una media y varianza muestral igual a 645 y 941. Se esperaba que la densidad de las colas en las atracciones disminuyera en los meses invernales.
De una muestra de 82 días observados durante diciembre, enero y febrero, se obtuvo la media y la varianza muestral siguientes: 268 y 512.
Obtener un intervalo de confianza del 90% para la diferencia de media de las personas en espera durante más de 20 minutos entre los meses de verano e invierno suponiendo que siguen una distribución normal.

Realizamos un recopilatorio de los datos ofrecidos en el enunciado del problema:

· X₁ ≡ 'Número de personas que esperan más de 20 minutos para entrar en cada atracción en verano'. Sigue una distribución Normal: X₁ = 645, S²₁ = 941, n₁ = 47.
· X₂ ≡ 'Número de personas que esperan más de 20 minutos para entrar en cada atracción en invierno: X₂ = 268, S²₂ = 512, n₂ = 82.

Nos pide realizar un intervalo de confianza para la diferencia de medias con varianzas desconocidas y n₁, n₂ ≥ 30:

Para un 90%, obtenemos α:

100(1 - α) = 90

Despejamos el parámetro que nos interesa: α = 0.1. El siguiente paso es obtener el valor de la z:

· z_α/2 = z_0.1/2 = z_0.05

Teniendo en cuenta las características de las tablas que dispone Aqueronte de la Normal, adecuamos dicho valor:

0.5 - 0.05 = 0.45

Es este caso, no está el valor exacto, por lo que realizamos una interpolación lineal:

..1.64.............Z..........1.65
0.4495........0.45.....0.4505

De donde:

1.64 - 1.65.---> 0.4495 - 0.4505
1.64 - Z..---> 0.4495 - 0.45

Calculamos:

Llegados a este punto, disponemos de todos los datos necesarios para obtener el intervalo de confianza al 90%, de la diferencia de medias con varianzas desconocidas y tamaños muestrales mayores o iguales a 30:

Por lo tanto, el intervalo de confianza es, aproximadamente, el que se muestra a continuación:

[368.569447, 385.430553]

Problema83: Estimación y Pruebas de Hipótesis

Ej83. Una profesora desea conocer si el porcentaje de aprobados en su asignatura ronda el 60% para comprobar si se cumplen los objetivos emprendidos al inicio del curso. Para comprobarlo, revisó las calificaciones de 100 estudiantes, de los que obtuvo un porcentaje del 57% de aprobados.

Si el error debe ser menor del 5%, ¿se cumplen los objetivos marcados por la profesora?.


Realizamos una recopilación de datos del problema:

· Tamaño de la muestra: n = 100.
· Proporción de aprobados: ṗ = 0.57.
· p_o = 0.6.

Para plantear la prueba de hipótesis debemos verificar las siguientes condiciones:

· n = 100 ≥ 30 OK.
· n·p_o = 100·0.6 = 60 ≥ 5 OK.
· n·(1-p_o) = 100·(1 - 0.6) = 40 ≥ 5 OK.

La prueba de hipótesis que debemos plantear es la siguiente:

Es un contraste sobre la proporción, el estadístico es:

Obtenemos el valor del estadístico:

Para comprobar si aceptamos o rechazamos la hipótesis nula, empleamos la región crítica, que para esta prueba es:

Z ≥ Z_α/2, Z ≤ -Z_α/2

El enunciado no nos ofrece un nivel de significación pero si nos da el error:

Sustituimos valores:

Despejamos Z_α/2 para obtener su valor:

· Z_α/2 ≤ 1.009946

Ya disponemos de todos los datos necesarios para dar una opinión estadística al problema. Comprobamos el valor del estadístico con la región crítica:

El valor del estadístico, -0.612372 está dentro de la región crítica, [-1.009946, 1.009946], por lo tanto, aceptamos la hipótesis nula.

Esto quiere decir, que existen evidencias significativas de que se cumplen los objetivos marcados por la profesora, el aprobado de su asignatura ronda el 60%.

Problem21: VAD

¡Puedes leer este texto en español! Problema21: VAD

Ej21. The proportion of patients who are cured of a disease through a treatment is equal to 0.8. If 20 patients of this disease are undergoing the treatment, what probability will there be that 18 patients will be cured?.


We conduct a data compilation given by problem statement:

· X ≡ 'Number of patients who are cured of a disease through a treatment'.
· The random variable X follows a Binomial distribution: X ~ B(20, 0.8).

We have to get the following probability:

P(X = 18) = ₂₀C₁₈·0.8¹⁸·(1-0.8)^20-18 ≈ 0.136909
Finally, the probability of being cured 18 patients with this treatment is 0.136909.

Problem43: Probability

¡Puedes leer este texto en español! Problema43: Probabilidad

Ej43. An urn A has 5 white balls and 5 black ones. Another urn B, has 3 white balls and 3 black ones. An urn is chosen at random and two balls are drawn at the same time.

Calculate the probability that both balls will be black.


We conduct a data compilation given by problem statement:

· Urn with letter A: 5 white balls and 5 black ones. Total: 5+5 = 10.
· Urn with letter B: 3 white balls and 3 black ones. Total: 3+3 = 6.

· N ≡ 'Both balls drawn are black'.
· A ≡ 'Ball drawn of the urn A'.
· B ≡ 'Ball drawn of the urn B'.

· P(A) = P(B) = 1/2.

The solution to this problem is as follows:

Finally, the probability of getting two consecutive black balls and without replacement is approximately, 0.211111.

Problem19: VAD

¡Puedes leer este texto en español! Problema19: VAD

Ej19. The number of surface defects of the plastic panels used inside the car, follows a Poisson distribution with value mean equal to 0.5 defects per square meter of panel.

If the inside the car has 4 square meter of this material then, which is the probability that there won't be any surface defects?.


We conduct a data compilation given by problem statement:

· X ≡ 'Number of surface defects of the plastic panels that are used inside the car'.
· The random variable X follows a Poisson distribution: X ~ P(0.5).

If a car has 4 m² of this material, we have to adapt the variable for this specification:

· Random variable X with 4 m²: X ~ P(4·0.5) = P(2).

We must get the following probability:

Finally, the probability that there won't be any surface defect of the plastic panels inside the car with 4 m² of this material is 0.135335.

Problem88: VAD

¡Puedes leer este texto en español! Problema88: VAD

Ej88. A company works to the production and sale of children's puzzle of 50 pieces each one. The probability that the puzzle has a print defect is 0.01 and a cut defect is 0.05.

It's possible that there are both defects independently at each piece. Calculate the average number of defectives pieces that exist at a children's puzzle.


We perform a data compilation given by problem statement:

· I ≡ 'A print defect'.
· C ≡ 'A cut defect'.

· P(I) = 0.01
· P(C) = 0.05

· D ≡ 'The piece is defect'.

· P(D) = P(I ∪ C) = P(I) + P(C) - P(I ∩ C) = 0.01 + 0.05 - 0.01·0.05 = 0.0595

· X ≡ 'Number of defectives pieces' X ~ B(50, 0.0595).

The random variable X follows a Binomial Distribution, so we apply the mean of this distribution:

· μ = n·p = 50·0.0595 = 2.975

Finally, the average number of defectives pieces is 2.975.

Problem14: Probability

¡Puedes leer este texto en español! Problema14: Probabilidad

Ej14. For some dice, the probability of being a face, when pulled, is proportional to the number of points that it showed. Calculate the probability of getting with this dice, an even number.

The sample space of the dice is:

Ω = {1, 2, 3, 4, 5, 6}

The probability of getting any value of the dice is proportional to its value.

So, we have to get all values that there in a dice:

Total points = 1+2+3+4+5+6 = 21

To get an element, its probability will be its value among the total points of the dice, in other words:

P(1) = 1/21, P(2) = 2/21, P(3) = 3/21, P(4) = 4/21, P(5) = 5/21, P(6) = 6/21

It creates the following event:

A Ξ “It's an even number”

The event A has the following elements:

A = {2, 4, 6}

And finally, the probability of event A, is the sum of the probabilities of all its components:

P(A)= P(2) + P(4) + P(6) = 2/21 + 4/21 + 6/21 = 12/21 = 4/7

Problem87: Probability

¡Puedes leer este texto en español! Problema87: Probabilidad

Ej87. A company makes a quality control to each batch of 16 engines. In the quality control, 2 engines are randomly selected (without replacement) of each batch of 16 engines and they are inspected.

If any of the two is defective, all the batch will be rejected but if none is defective, the 16 engines will be accepted and they will send for sell.

If it is inspected a batch of 16 engines which only has one defective, calculate the probability that the batch is rejected .


We perform a data compilation given by the problem statement

· It will randomly select two engines (without replacement) from a total of 16.
· It assumes that the engines are independent: P(X_n ∩ X_m) = 0
· X_i ≡ 'Defective i-Engine'.

· P(X_i) = 1/16.

We have to get the following probability:

P(X₁ ∪ X₂) = P(X₁) + P(X₂) = 1/16 + 1/16 = 1/8

So, the probability that the batch will be rejected (any of the engines is defective) is 0.125.

Problem81: Confidence Interval

¡Puedes leer este texto en español! Problema81: EYPH

Ej81. The personnel department of some company, wants to apply a discount to the insurance of those employees whose spending is less than 150 € as long as this porcion is not very high.

For this purpose, it took a sample of 100 employees of whom, 20 employees had spending less than 150 €.

Estimate a 95% confidence interval for proportion of employees with spending less than 150 €.


We perform a data collection given by problem statement:

· X ≡ 'Proportion of employees with spending less than 150€'.
· P(X) = 20/100 = 1/5.

We have to make a confidence interval of proportion but before we must check the following conditions:

· n = 100 ≥ 30 OK.
· n·p = 100·1/5 = 20 ≥ 5 OK.
· n·q = 100·(1-1/5) = 80 ≥ 5 OK.

It obtains the α-parameter: 100(1 - α) = 95, We solve: α = 0.05.

· z_0.05/2 = z_0.025

We have to consider conditions of the Normal table, so we have to adapt the value:

0.5 - 0.025 = 0.475

Looking in the Normal table, we obtain the following value: 1.96.

The confidence interval of proportion has the following mathematical expression:

Now, we have all necessary data to make a 95% confidence interval of proportion of employees whose spending is less than 150€, we just replace values:

Finally, the problem solution is:

[0.1216, 0.2784]