Ej83. Una profesora desea conocer si el porcentaje de aprobados en su asignatura ronda el 60% para comprobar si se cumplen los objetivos emprendidos al inicio del curso. Para comprobarlo, revisó las calificaciones de 100 estudiantes, de los que obtuvo un porcentaje del 57% de aprobados.
Si el error debe ser menor del 5%, ¿se cumplen los objetivos marcados por la profesora?.
Realizamos una recopilación de datos del problema:
· Tamaño de la muestra: n = 100.
· Proporción de aprobados: ṗ = 0.57.
· po = 0.6.
Para plantear la prueba de hipótesis debemos verificar las siguientes condiciones:
· n = 100 ≥ 30 OK.
· n·po = 100·0.6 = 60 ≥ 5 OK.
· n·(1-po) = 100·(1 - 0.6) = 40 ≥ 5 OK.
La prueba de hipótesis que debemos plantear es la siguiente:
Es un contraste sobre la proporción, el estadístico es:
Obtenemos el valor del estadístico:
Para comprobar si aceptamos o rechazamos la hipótesis nula, empleamos la región crítica, que para esta prueba es:
El enunciado no nos ofrece un nivel de significación pero si nos da el error:
Sustituimos valores:
Despejamos Zα/2 para obtener su valor:
· Zα/2 ≤ 1.009946
Ya disponemos de todos los datos necesarios para dar una opinión estadística al problema. Comprobamos el valor del estadístico con la región crítica:
El valor del estadístico, -0.612372 está dentro de la región crítica, [-1.009946, 1.009946], por lo tanto, aceptamos la hipótesis nula.
Esto quiere decir, que existen evidencias significativas de que se cumplen los objetivos marcados por la profesora, el aprobado de su asignatura ronda el 60%.

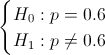
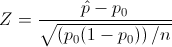
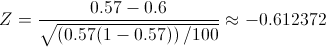
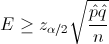
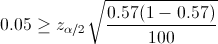





2 comentarios:
Buenas Tardes Manuel:Gracias por compartir tus conocimientos en tu blog, yo estoy cursando mi maestria en este momento, y en la clase de Estadistica me sentia bastante confundido, he consultado en libros e internet , y buscando encontre tu blog, el cual me parece muy bueno,con tus ejemplos he aclarado muchas dudas que tenia, te queria consultar si tenes algun ejercicio para obtener intervalos de confianza o me podes ayudar a resolver un ejercicio sobre ese tema?(disculpa si este tema no pertenece a esta categoria,estuve buscando pero no encontre las categorias),tengo un ejercicio que resolver,pero para ser sincero me siento muy confundido con ese tema,te cuento el ejercicio: Se necesita una estimacion del tiempo de espera en las atracciones de un parque tematico porque existe una preocupacion con respecto a una posible bancarrota de la empresa, sino se agilizan las colas. El numero de personas que esperan mas de 20 minutos para entrar a cada atraccion, registrado durante n=47 dias en julio y agosto,tuvo respectivamente una media y varianza muestral igual a 654 y 941.Se esperaba que la densidad de las colas en las atracciones disminuyera en los meses invernales.De una muestra de n=82 dias observados durante diciembre,enero y febrero,se obtuvo la media y la varianza siguientes: 268 y 512.Obtener un intervalo de confianza del 90% para diferencia en la densidad media de las personas en espera durante mas de 20 minutos entre los meses de verano e invierno.
Gracias por tu ayuda y saludos desde Rosario, Argentina.
Angel Rodriguez.
Buenas Ángel Rodríguez:
He incorporado el problema que indicas en el boletín de problemas que tenemos en Aqueronte, concretamente es el Problema 84 ya que no había ninguno resuelto de estas características (sí similares).
Para encontrar las categorías o el curso de estadística en el blog, es fácil, en el menú de la izquierda busca Estadística y dentro encontrarás el curso, dónde hay un apartado llamado: Estimación, Intervalos de Confianza y Pruebas de Hipótesis.
Un saludo y gracias por tu comentario.
Publicar un comentario