Ej84. Se necesita una estimación del tiempo de espera en las atracciones de un parque temático ya que existe una preocupación con respecto a una posible bancarrota de la empresa sino se agilizan las colas.
El numero de personas que esperan mas de 20 minutos para entrar a cada atracción, registrado durante 47 días en julio y agosto, tuvo, respectivamente, una media y varianza muestral igual a 645 y 941. Se esperaba que la densidad de las colas en las atracciones disminuyera en los meses invernales.
De una muestra de 82 días observados durante diciembre, enero y febrero, se obtuvo la media y la varianza muestral siguientes: 268 y 512.
Obtener un intervalo de confianza del 90% para la diferencia de media de las personas en espera durante más de 20 minutos entre los meses de verano e invierno suponiendo que siguen una distribución normal.
Realizamos un recopilatorio de los datos ofrecidos en el enunciado del problema:
· X1 ≡ 'Número de personas que esperan más de 20 minutos para entrar en cada atracción en verano'. Sigue una distribución Normal: X1 = 645, S21 = 941, n1 = 47.
· X2 ≡ 'Número de personas que esperan más de 20 minutos para entrar en cada atracción en invierno: X2 = 268, S22 = 512, n2 = 82.
Nos pide realizar un intervalo de confianza para la diferencia de medias con varianzas desconocidas y n1, n2 ≥ 30:
Despejamos el parámetro que nos interesa: α = 0.1. El siguiente paso es obtener el valor de la z:
· zα/2 = z0.1/2 = z0.05
Teniendo en cuenta las características de las tablas que dispone Aqueronte de la Normal, adecuamos dicho valor:
Es este caso, no está el valor exacto, por lo que realizamos una interpolación lineal:
..1.64.............Z..........1.65
0.4495........0.45.....0.4505
De donde:
1.64 - 1.65.---> 0.4495 - 0.4505
1.64 - Z..---> 0.4495 - 0.45
Calculamos:
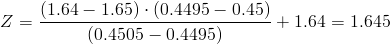
Por lo tanto, el intervalo de confianza es, aproximadamente, el que se muestra a continuación:

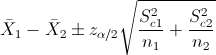
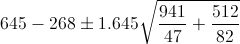




2 comentarios:
Creo que el resultado está mal debido a que en el enunciado dices que la media muestral es 654, sin embargo, después utilizas 645.
Buenas:
Tienes razón, se me ha bailado un número. Vamos hacer una cosa, para no tener que actualizar los datos del desarrollo del problema, vamos a considerar que la media muestral es de 645.
Aún así, el resultado final con la media muestral de 654 sería el siguiente:
· [377.569447, 394.430534]
Un saludo y gracias por la corrección.
Publicar un comentario