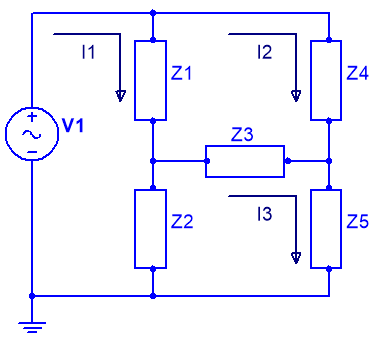
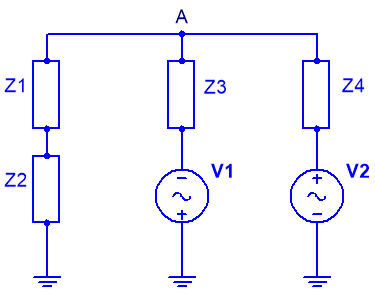
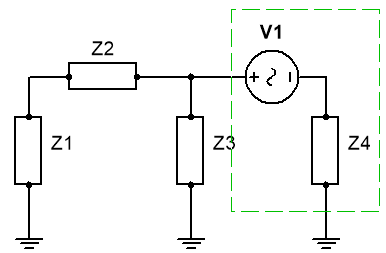
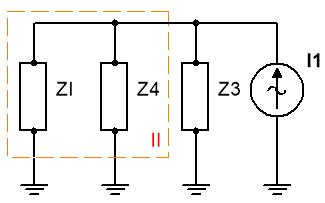
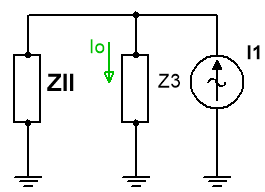
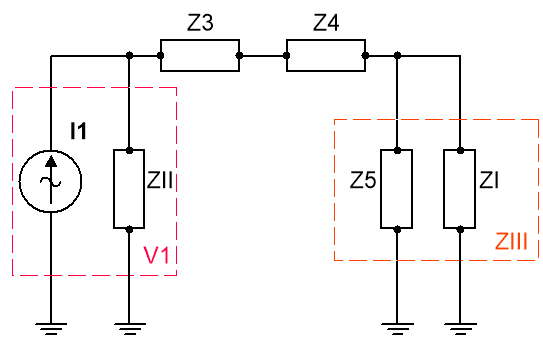
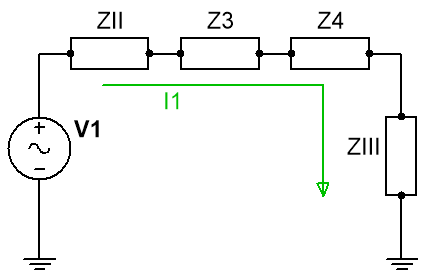
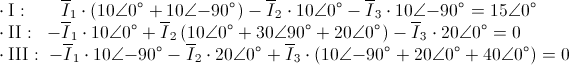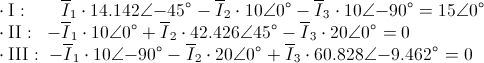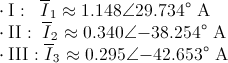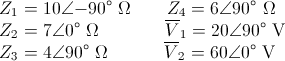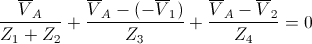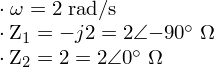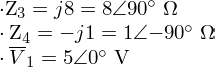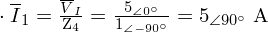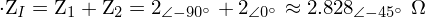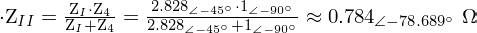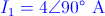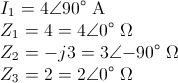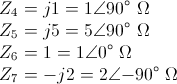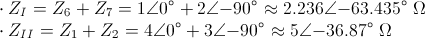Ej10. Dado el circuito de la figura:
Donde:
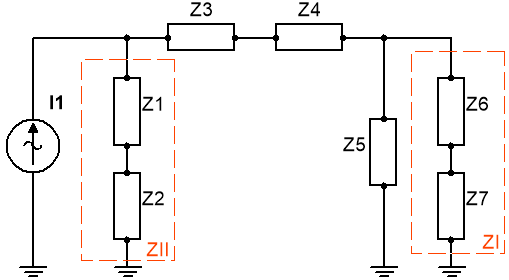
· Z1 = 10 Ω
· Z2 = -j10 Ω
· Z3 = 20 Ω
· Z4 = j30 Ω
· Z5 = 40 Ω
· v1(t) = 15·cos(4t) V
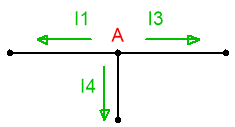
Obtener el valor de las corrientes señaladas en el circuito anterior: I1, I2 e I3.
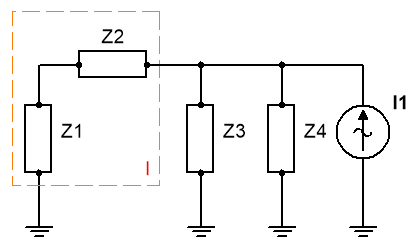
Pasamos todos los componentes al estado Fasor (modo polar):
Donde:
· w = 4 rad/s.
Vamos a resolver el circuito realizando un estudio de mallas (las que se muestran en la figura del circuito del enunciado del problema):
· MALLA I (I1):
· -V1 + I1·(Z1 + Z2) - I2·Z1 - I3·Z2 = 0
· MALLA II (I2):
· I2·(Z1 + Z4 + Z3) - I1·Z1 - I3·Z3 = 0
· MALLA III (I3):
· I3·(Z2 + Z3 + Z5) - I1·Z2 - I2·Z3 = 0
Reordenamos la expresión anterior y sustituimos valores:
Simplificamos:
Llegados a este punto, tenemos tres ecuaciones con tres incógnitas, resolvemos para obtener la solución a este problema:
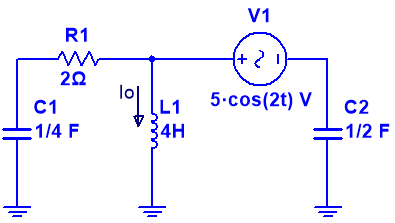
Os dejo una simulación realizada en LTSpice:
| Problema 10: Régimen Permanente Senoidal | ||||||
|
Se ha optado la representación polar frente a la rectangular por comodidad a la hora de representar las operaciones y expresiones matemáticas.