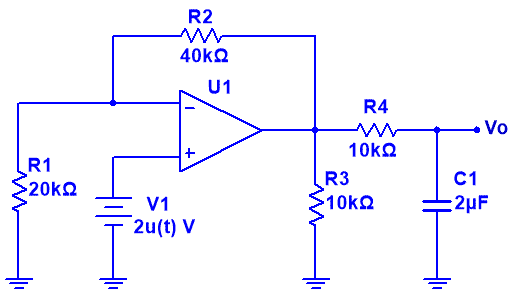
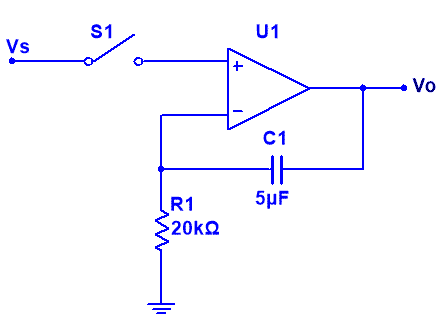
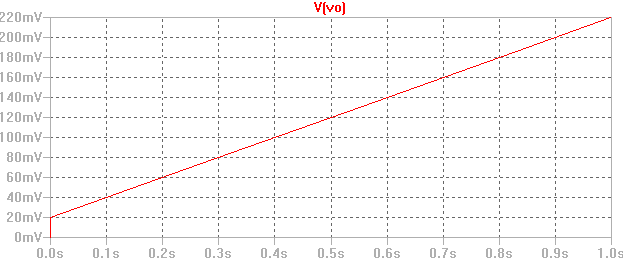
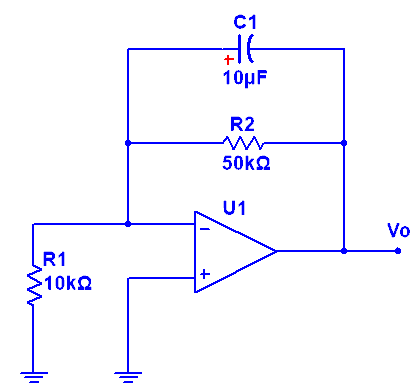
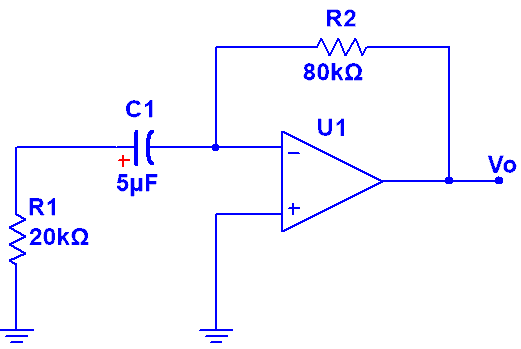
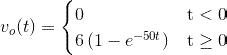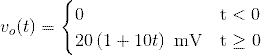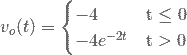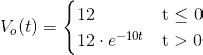Ej6. En interruptor del circuito de la figura ha estado abierto durante un largo periodo de tiempo, en el instante t = 0 se cierra, considerando que el amplificador operacional es ideal.
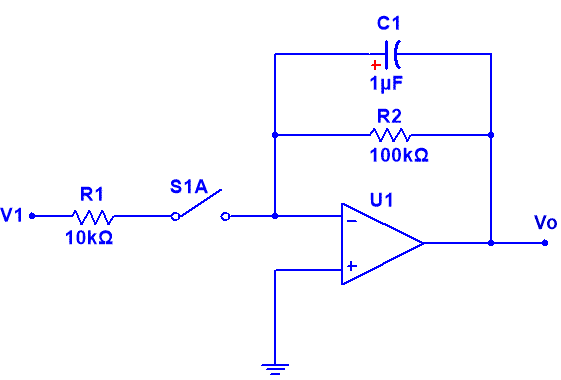
El enunciado nos indica que el interruptor ha estado abierto durante un largo periodo de tiempo, esto quiere decir que el condensador está totalmente descargado y por lo tanto, el instante t < 0, el valor de salida vo (t) = 0 V.
Ahora nos falta resolver el circuito para el instante t > 0.
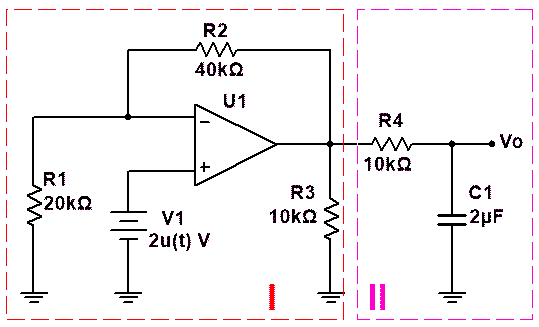
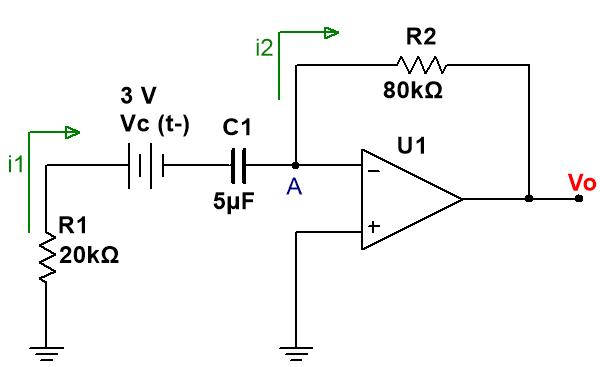
El circuito es el que se puede observar en la siguiente figura:
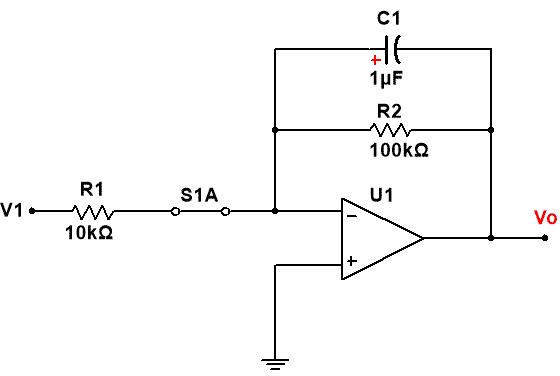
Al estar presente un condensador, el circuito constará de dos partes, éstas son: Régimen permanente y Régimen transitorio, así que vamos a obtener los resultados de ambas partes para posteriormente, dar la solución a este problema.
· Régimen Permanente:
En el régimen permanente, se considera que ya ha pasado un largo período de tiempo y por lo tanto, el condensador le ha dado tiempo de cargarse completamente. Un condensador cargado en DC, se comporta como un circuito abierto.
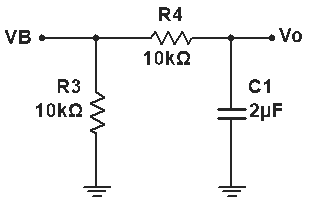
Por lo tanto, el circuito resultante es el siguiente:
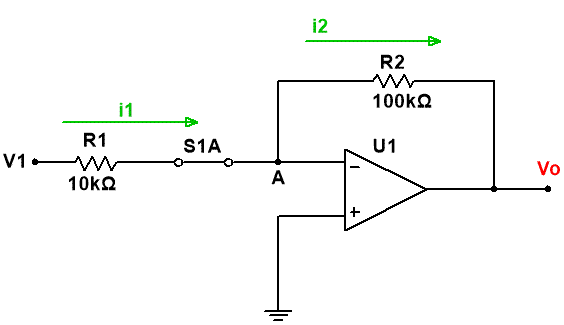
Otra información que nos proporciona el enunciado del problema es que el amplificador operacional es ideal, esto quiere decir que:
· V- = V+ = VA = 0 V
Prestamos atención al Nodo A: i1 = i2
Donde:
· i1 = ( V1 - VA )/R1 = V1/R1
· i2 = ( VA - vOp )/R2 = - vOp/R2
Por lo tanto:
· V1/R1 = - vOp/R2
Obtener el valor de la tensión de salida es fácil:
· vOp = - ( R2/ R1 )·V1
Sustituimos valores:
· vOp = - ( 100·103/10·103 )·4·10-3 = - 40 mV.
· Régimen Transitorio:
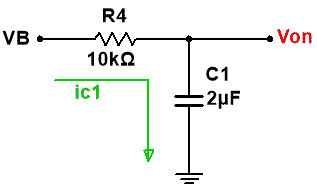
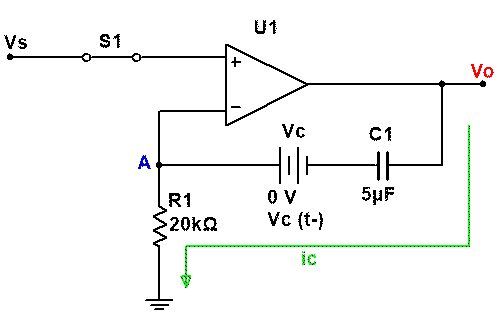
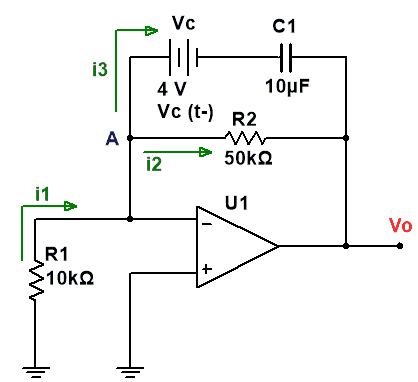
El circuito resultante es el siguiente:
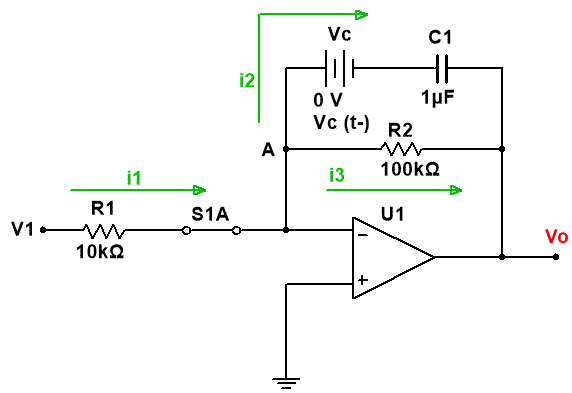
· NOTA: Se ha aplicado la técnica del condensador equivalente, una fuente de tensión con el valor de la carga inicial del condensador, en serie con un condensador sin carga de la misma capacidad que el original.
Otra información que nos proporciona el enunciado del problema es que el amplificador operacional es ideal, esto quiere decir que:
· V- = V+ = VA = 0 V
Prestamos atención al Nodo A: [Ec1] i1 = i2 + i3
Donde:
· i1 = ( V1 - VA )/R1 = V1/R1
· i2 = ( VA - vOn )/R2 = - vOn/R2
· i3 = iC1 = C1DvC1 = { vC1 = VA - vOn = - vOn } = - C1DvOn
Sustituimos valores en [Ec1]:
· V1/R1 = - C1DvOn - vOn/R2
Manipulamos la expresión dividiendo por C1:
· DvOn + 1/( R2C1 )·vOn = - V1/( R1C1 )
Llegados a este punto, ya tenemos nuestra ecuación diferencial de 1º Orden, la homogénea es la siguiente:
· [Ec2] DvOn + 1/( R2C1 )·vOn = 0
Por teoría, sabemos que una solución a la ecuación diferencial homogénea de 1º Orden es:
· vOn (t) = k·e-A·t
· DvOn (t) = -kA·e-A·t
Sustituimos en [Ec2]:
Analizamos el circuito en el instante t = 0, por lo tanto:
Despejamos el parámetro A:
· A = 1/( R2C1 ) = 1/( 100·103·1·10-6 ) = 10 s-1
Por lo tanto, la constante de tiempo es:
· τ = 1/A = 1/10 = 0.1 s
Una vez obtenido el parámetro A, vamos a obtener el parámetro k, para ello, trabajaremos con la expresión del voltaje de salida completa:
· vO (t) = vOp (t) + vOn (t) = - 40·10-3 + k·e-10t
Aplicaremos la condición del condensador:
· Condensador: La tensión no puede cambiar bruscamente en un instante concreto.
Esto quiere decir lo siguiente, en el instante t = 0:
· vC1(0-) = vC1(0+) = 0 V
Y teniendo en cuenta que la tensión del condensador es la misma pero con signo contrario, a la tensión de salida:
· vC1 = VA - vOn = - vOn
Por lo tanto, tenemos lo siguiente:
· - 0 = - 40·10-3 + k·e-10·0
Despejamos el parámetro k:
· k = 40·10-3
Así que, la solución a este problema es la siguiente:
· vO (t) = vOp (t) + vOn (t) = - 40·10-3 + 40·10-3·e-10t = 40·( e-10t - 1 ) mV, t >0
En modo resumen, la expresión matemática o la evolución de la tensión de salida vO( t ) teniendo en cuenta las circunstancias dadas, es la siguiente:
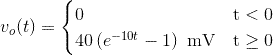
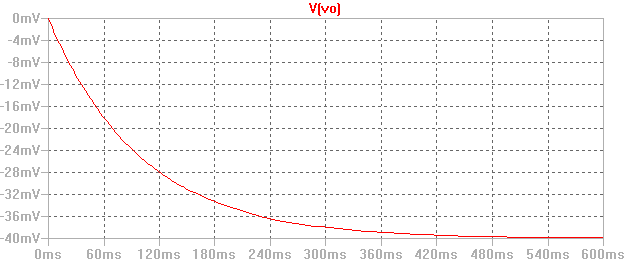
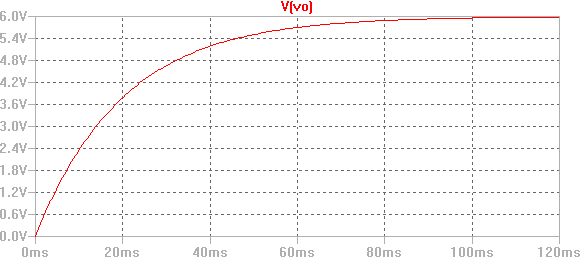
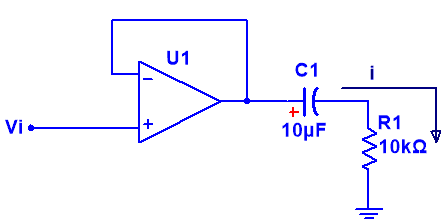
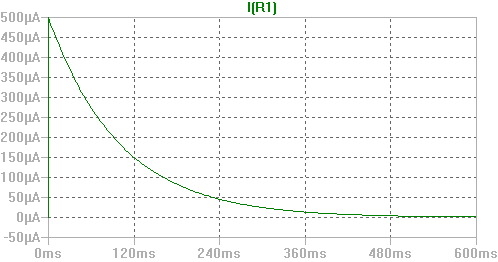
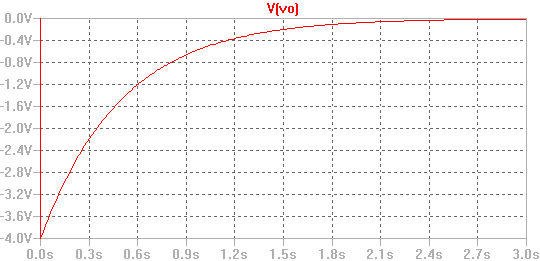
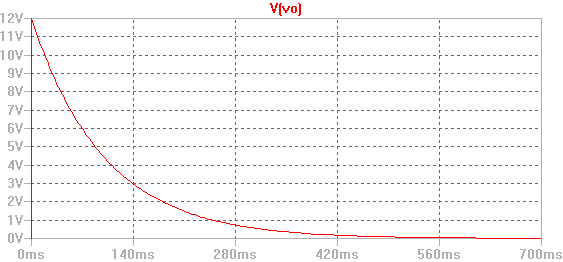
Os dejo una simulación realizada en LTSpice:
| Problema 6: Transitorios de 1º Orden ( Amplificador Operacional IDEAL ) | ||||||
|