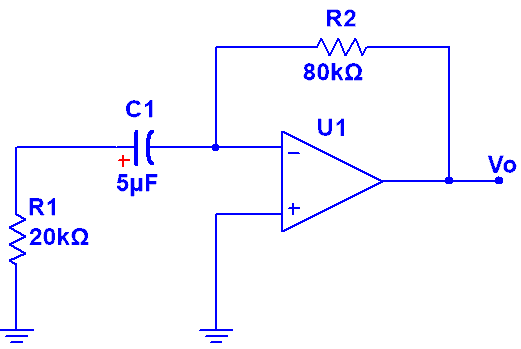
Ej1. Teniendo en cuenta que el condensador presenta una carga inicial de 3V y considerando que el amplificador operacional es ideal.
Obtener la tensión de salida vo( t ).
En este problema no tenemos ninguna fuente de excitación, simplemente nos dicen que el condensador presenta una carga inicial, así que, vamos a adaptar el circuito resultante para empezar a resolver el problema y para ello, sabemos que el equivalente a un condensador cargado es el valor de su tensión en serie, con un condensador equivalente del mismo valor pero sin carga.
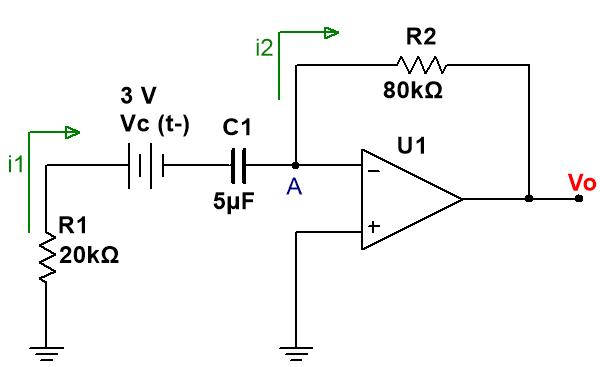
Por lo tanto, el circuito resultante es el que se muestra a continuación:
Otra información que nos proporciona el enunciado del problema es que el amplificador operacional es ideal, esto quiere decir que:
· V- = V+ = VA = 0
· i1 = i2 = iC1.
Dicho de otra manera:
· El nodo V+ del amplificador operacional está conectado a tierra, por lo que su valor es cero, eso quiere decir que el nodo negativo es cero también, y en nuestro caso: V- = VA.
· Y la única corriente del circuito es la proporcionada por el condensador.
Bien, teniendo en cuenta dichas premisas, vamos a resolver el circuito en torno al nodo A.
· NOTA: Antes de entrar en cálculos, sabemos que circuitos de este tipo: Transitorios de 1º Orden, se debe obtener tanto el régimen transitorio como el régimen permanente, pero en nuestro caso, el régimen permanente es obvio, su valor es cero ( vp= 0 V ) ya que el condensador se descargará completamente y no existe ninguna fuente de excitación para volverlo a cargar.
Así que centraremos los datos en el condensador y en este caso, en el régimen transitorio.
· Corriente i1:
Realizamos el análisis mediante LVK:
· [Ec1] vn + i1·R1 + ( vC(t-) + VA ) = 0
Dónde:
· ic = C1·Dvn
· V- = V+ = VA = 0
Sustituimos el valor en [Ec1] y dividimos por C1·R1:
· Dvn + [1/(C1·R1)]·Vn = - V1/(C1·R1)
Ya tenemos nuestra ecuación diferencial de 1º Orden, la ecuación homogénea es:
· [Ec2] Dvn + [1/(C1·R1)]·vn = 0
Por teoría, sabemos que una solución a la ecuación diferencial homogénea de 1º Orden es:
· vn(t) = k·e-A·t
· Dvn(t) = - kA·e-A·t
Sustituimos en [Ec2]:
- k·A·e-A·t + [1/(C1·R1)]·k·e-A·t = 0
Analizamos en circuito en el instante t = 0, por lo tanto:
- k·A + [1/(C1·R1)]·k = 0
Despejamos el parámetro A:
· A = 1/( C1·R1 ) = 1/( 5·10-6 · 20·103 ) = 10 s-1
Por lo tanto, la constante de tiempo en el instante t = 0 es:
· τ = 1/A = 1/10 = 0.1 s
Una vez obtenido el parámetro A, vamos a obtener el valor del parámetro k, para ello, aplicamos la condición del condensador.
· Condensador: La tensión no puede cambiar bruscamente en un instante concreto.
Según el enunciado del problema, el condensador presenta una carga inicial de 3 V:
· vC(0-) = 3 V
En el instante t = 0:
· vC(0-) = vC(0+)
Por lo tanto:
· 3 = vp + vn = 0 + k·e-10t = {t = 0} = k
Despejamos k:
· k = 3
Así que, una expresión para la tensión del condensador es:
· vC(t) = 3·e-10t V, t > 0
· Corriente i2:
Realizamos el análisis mediante LVK:
· [Ec3] ( VA - vo )/R2 = iC
Dónde:
· iC = C1·Dvn
· V- = V+ = VA = 0
Sustituimos el valor en [Ec3] y dividimos por C1:
· Dvn = - vo/( C1·R2 )
Despejamos el parámetro que nos interesa, vo:
· vo = - C1·R2·Dvn
En estos momentos disponemos del valor de la tensión del condensador, así que sustituimos para aplicar la derivada:
· vo = - C1·R2·Dvn = - C1·R2·D( 3·e-10t ) = - C1·R2·( - 30·e-10t )
Sustituimos valores para obtener la solución de este problema:
· vo = - C1·R2·( - 30·e-10t ) = - ( 5·10-6 · 80·103 )·( - 30·e-10t ) = - 0.4·( - 30·e-10t ) = 12·e-10t
En modo resumen, la expresión matemática o la evolución de la tensión de salida vo( t ) dadas las circunstancias dadas, es la siguiente:
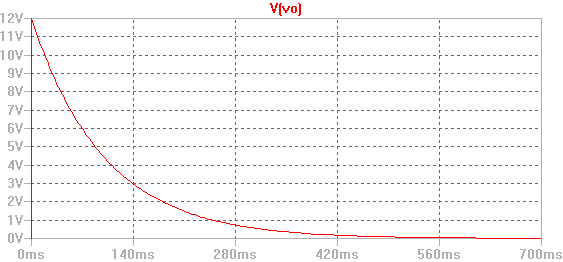
Cuya representación gráfica es la que se muestra a continuación:
Os dejo una simulación realizada en LTSpice:
| Problema 1: Transitorios de 1º Orden ( Amplificador Operacional IDEAL ) | ||||||
|

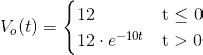







0 comentarios:
Publicar un comentario