Aqueronte: Problema3: Circuitos de 1º Orden Amplificadores Operacionales

Ej3. Teniendo en cuenta que el condensador presenta una carga inicial de -2 V y considerando que el amplificador operacional es ideal.

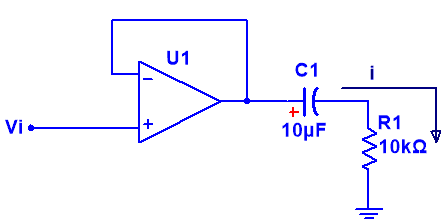
Obtener la corriente de salida i( t ) siendo v_i = 3·u(t).

La tensión de entrada v_i, es una función escalón unitario, o lo que es lo mismo, como vamos a trabajar en el instante t = 0, dicha función escalón, antes de dicho instante su valor será: v_i = 0 V, y en el instante t = 0, su valor será: v_i = 3 V.

Otro dato interesante que nos ofrece el enunciado del problema es que el condensador presenta una carga inicial, así que plantearemos el circuito equivalente teniendo en cuenta que si el condensador está cargado inicialmente, su equivalente es una fuente de tensión con el valor de la carga en serie con un condensador del mismo valor pero sin carga.

Por lo tanto, el circuito resultante es el que se muestra a continuación:

Otra información que nos proporciona el enunciado del problema es que el amplificador operacional es ideal, esto quiere decir que:

· V^- = V⁺= V_i= 3·u(t) V

· NOTA: Antes de entrar en cálculos, sabemos que circuitos de este tipo: Transitorios de 1º Orden, se debe obtener tanto el régimen transitorio como el régimen permanente, pero en nuestro caso, el régimen permanente es obvio, su valor es cero ( i_p= 0 A ) ya que el condensador se cargará y actuará como un circuito abierto.

Así que centraremos los datos en el condensador y en este caso, en el régimen transitorio.

Realizamos el análisis mediante LVK:

· [Ec1] -V^- + V_C + V_C1+ V_R1= 0

Donde:

· V_C1= 1/( C₁·D)·( i_n )
· V_R1= i_n·R₁

Sustituimos valores en [Ec1]:

· -V^- + V_C + 1/( C₁·D )·( i_n )+ i_n·R₁= 0

Manipulamos la expresión multiplicando por el parámetro D y dividiendo por R₁:

· Di_n + [ 1/( C₁·R₁) ]·i_n = D[ ( V^- - V_C )/R₁ ]

Ya tenemos nuestra ecuación diferencial de 1º Orden, la ecuación homogénea es:

· [Ec2] Di_n + [ 1/( C₁·R₁) ]·i_n = 0

Por teoría, sabemos que una solución a la ecuación diferencial homogénea de 1º Orden es:

· i_n(t) = k·e^-A·t
· Di_n(t) = - kA·e^-A·t
Sustituimos en [Ec2]:

- k·A·e^-A·t + [ 1/( C₁·R₁) ]·k·e^-A·t = 0

Analizamos en circuito en el instante t = 0, por lo tanto:

- k·A + [ 1/( C₁·R₁) ]·k = 0

Despejamos el parámetro A:

· A = 1/( C₁·R₁) = 1/( 10·10^-6· 10·10³) = 10 s^-1

Por lo tanto, la constante de tiempo en el instante t = 0 es:

· τ = 1/A = 1/10 = 0.1 s

Una vez obtenido el parámetro A, vamos a obtener el valor del parámetro k, para ello, aplicamos la condición del condensador.

· Condensador: La tensión no puede cambiar bruscamente en un instante concreto.

Según el enunciado del problema, el condensador presenta una carga inicial de -2 V:

· v_C(0^-) = -2 V

En el instante t = 0:

· v_C(0^-) = v_C(0⁺)

Pero en nuestro caso, no estamos resolviendo el problema en función del condensador, sino en función de la corriente de salida, así que deberemos buscar la forma de poner todo en función de dicha corriente de salida, y para ello, sabemos que la corriente final será la suma de la corriente permanente más la corriente transitoria:

· i(t) = i_p + i_n = 0 + i_n = i_n

Por lo tanto:

· [Ec3] i(t) = i_n= C₁·D·( v_C )

Donde:

· i_n= k·e^-10·t
· v_C= -V^-+ v_C= -3·u(t) + v_C= {t = 0} = -3·1 + (-2) = - 3 - 2 = -5 V

Sustituimos en [Ec3]:

· k·e^-10·t= C₁·D·( -V^-+ v_C )

Dividimos por el parámetro D:

· 1/D·( k·e^-10·t) = C₁·( -V^-+ v_C )

Realizamos la integral ( es inmediata ):

· -( k/10 )·e^-10·t = C₁·( -V^-+ v_C )

Analizamos en t = 0:

· -( k/10 ) = C₁·( -5 )

Sustituimos valores y despejamos k:

· k = 10·5·10·10^-6= 0.5·10^-3

Así que, una expresión para la corriente es:

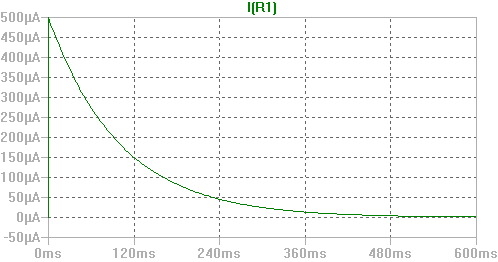
· i(t) = i_p + i_n = 0 + i_n = i_n= 0.5·e^-10·tmA, t > 0

En modo resumen, la expresión matemática o la evolución de la corriente de salida i( t ) dadas las circunstancias dadas, es la siguiente: