Problema81: Estimación y Pruebas de Hipótesis

You also can read this text in English! Problem81: EYPH

Ej81. El departamento de personal de cierta compañía, quiere implementar un descuento en el costo del seguro para aquellos empleados con gasto inferior a 150 euros siempre y cuando esta porción no sea muy elevada. Para ello se tomó una muestra de 100 empleados, 20 de los cuales tuvieron un gasto inferior a 150 euros.

Estimar mediante un intervalo de confianza del 95% la proporción de empleados con un gasto inferior a 150 euros.


Realizamos un recopilatorio de los datos ofrecidos en el enunciado del apartado:

· X ≡ 'Proporción de empleados con un gasto inferior a 150€'.
· P(X) = 20/100 = 1/5.

Nos piden realizar un intervalo de confianza de proporción, debemos verificar las siguientes condiciones:

· n = 100 ≥ 30 OK.
· n·p = 100·1/5 = 20 ≥ 5 OK.
· n·q = 100·(1-1/5) = 80 ≥ 5 OK.

Obtenemos el parámetro α: 100(1 - α) = 95, despejamos: α = 0.05.

· z_0.05/2 = z_0.025

Teniendo en cuenta las condiciones de la tabla de la Normal que se exponen en este blog:

0.5 - 0.025 = 0.475

Buscamos en la tabla de la Normal y el valor obtenido es 1.96.

El intervalo de confianza a obtener es el siguiente:

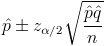
Ya disponemos de todos los datos necesarios para realizar un intervalo de confianza para la proporción de empleados con un gasto inferior a 150€ al 95%, simplemente, sustituimos valores:

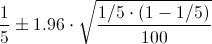
El intervalo de confianza es:

[0.1216, 0.2784]