Ej80. En el departamento de personal de una gran compañía se quiere estimar los gastos familiares en asistencia médica de sus empleados para determinar la posibilidad de proporcionarles un plan de seguro médico.
Se puede suponer que la variable X = 'Gasto en asistencia médica de los empleados' sigue una distribución normal. Si el gasto en asistencia médica de 10 empleados elegidos al azar fue:110. 362. 246. 85. 510. 208. 173. 425. 316. 179
a) Estimar mediante un intervalo de confianza del 95% el verdadero gasto promedio en asistencia médica.
b) Estimar mediante un intervalo de confianza del 95% la desviación típica de los gastos en asistencia médica.
En este problema, nos dan los datos de una muestra aleatoria, por lo que tenemos que obtener la media y la cuasi desviación estándar.
Para obtener la media:
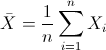
Por lo tanto:
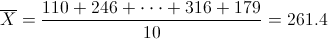
Para obtener la cuasi varianza:
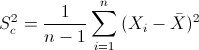
Por lo tanto, la cuasi desviación típica:
Ya estamos en condiciones para resolver los apartados que nos ofrece el enunciado del problema.
Apartado a)
En este problema nos pide realizar un intervalo de confianza para la media con varianza desconocida y el tamaño de la muestra es menor que 30:
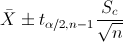
Para una confianza del 95%, obtenemos α:
Despejamos el parámetro que nos interesa: α = 0.05. El siguiente paso es obtener el valor de la t:
Por lo tanto, ya disponemos de todos los datos necesarios para realizar un intervalo de confianza de la media con un 95%, simplemente, sustituimos valores:
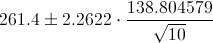
El intervalo de confianza bilateral al 95% es:
Apartado b)
En este problema nos pide realizar un intervalo de confianza para la varianza con la media desconocida:
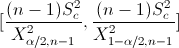
Para una confianza del 95%, obtenemos α:
Despejamos el parámetro que nos interesa: α = 0.05. El siguiente paso es obtener los valores de:
· X21-α/2,n-1 = X21-0.05/2, 10-1 = X20.975, 9
Buscamos el valor en la tabla ji-cuadrada, y obtenemos: 19.02 y 2.70 respectivamente.
Por lo tanto, ya disponemos de todos los datos necesarios para realizar un intervalo de confianza de la varianza con media desconocida y al 95%, simplemente, sustituimos valores:
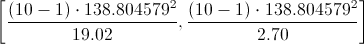





0 comentarios:
Publicar un comentario