Ej74. Una máquina A produce y envasa cierto producto a razón de 100 unidades por caja. Cada unidad tiene un peso N(8, 3) gramos. Otra máquina B hace lo mismo pero el peso de cada unidad es uniforme entre 5 y 11 gramos.
Una norma indica que una caja debe pesar entre 760 y 840 gramos.
Hallar la probabilidad de que una caja procedente de la máquina A sea rechazada y la probabilidad de que una caja procedente de la máquina B sea rechazada.
Realizamos una recopilación de datos que nos ofrece el problema:
· A ≡ 'Máquina A que produce y envasa cierto producto'.
· B ≡ 'Máquina B que produce y envasa cierto producto'.
Dichas variables siguen las distribuciones siguientes:
· A ~ N(8, 3) gramos/unidad.
· B ~ U(5, 11) gramos/unidad.
Hay que tener en cuenta que una caja consta de 100 unidades para ambas máquinas, por lo que nuestras variables aleatorias se deben ajustar a dicha cantidad:
· A ~ N(8·100, 3·100) = N(800, 300).
Para el evento B, vamos a obtener la media y su varianza para una caja teniendo en cuenta que es una distribución uniforme:
La media de la distribución uniforme viene dada por:
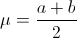
Por lo tanto, el valor de la media es:
Y la varianza de la distribución uniforme viene expresada por:
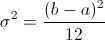
Sustituimos valores para obtener la varianza:
Podemos representar el evento B como una distribución Normal con los siguientes parámetros:
· B ~ N(800, 300).
Vemos que tanto el evento A cómo el B son iguales, por lo que ambos tendrán la misma probabilidad de que la caja sea rechazada.
Debemos obtener la siguiente probabilidad:
Tipificamos:
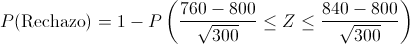
Manipulamos la expresión:
Operamos:
Buscamos en las tablas de la Normal expuestas en este blog, para dar cómo resultado final:
Por lo tanto, la probabilidad de que una caja procedente de la caja A o de la caja B sea rechazada es de 0.0208.





1 comentarios:
Buenas,
Me gustaria saber porque utilizas la varianza cuando aplicas la normal a la uniforme.
Felicitarte por el blog
Publicar un comentario