Problem81: Confidence Interval

¡Puedes leer este texto en español! Problema81: EYPH

Ej81. The personnel department of some company, wants to apply a discount to the insurance of those employees whose spending is less than 150 € as long as this porcion is not very high.

For this purpose, it took a sample of 100 employees of whom, 20 employees had spending less than 150 €.

Estimate a 95% confidence interval for proportion of employees with spending less than 150 €.


We perform a data collection given by problem statement:

· X ≡ 'Proportion of employees with spending less than 150€'.
· P(X) = 20/100 = 1/5.

We have to make a confidence interval of proportion but before we must check the following conditions:

· n = 100 ≥ 30 OK.
· n·p = 100·1/5 = 20 ≥ 5 OK.
· n·q = 100·(1-1/5) = 80 ≥ 5 OK.

It obtains the α-parameter: 100(1 - α) = 95, We solve: α = 0.05.

· z_0.05/2 = z_0.025

We have to consider conditions of the Normal table, so we have to adapt the value:

0.5 - 0.025 = 0.475

Looking in the Normal table, we obtain the following value: 1.96.

The confidence interval of proportion has the following mathematical expression:

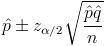
Now, we have all necessary data to make a 95% confidence interval of proportion of employees whose spending is less than 150€, we just replace values:

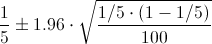
Finally, the problem solution is:

[0.1216, 0.2784]