ClassPad 330: Laplace

Una de las posibilidades que ofrece esta calculadora es la de obtener Transformadas y Antitransformadas de Laplace, este capítulo pretende ser una breve guía esquemática de como proceder para conseguir tal fin.

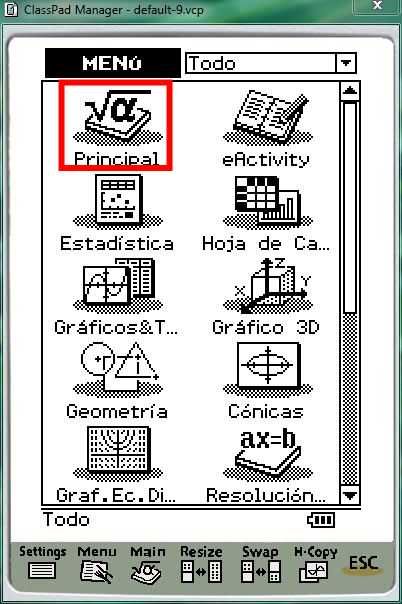
Los pasos a seguir serán los siguientes: Primero, debemos encender nuestra calculadora y en la pantalla de Menú, pulsar sobre Principal.

Ésto nos llevará a la ventana de cálculo que ofrece esta calculadora:

En la ClassPad 330 existen varias maneras de trabajar con la herramienta Transformada y Antitransformada de Laplace, podemos trabajar mediante la barra de herramienta tanto en Acción cómo en Interactivo, ofrecen la opción de Avanzado y desde ahí, están visibles y presentes las herramientas que deseamos.

Esta guía lo hará de manera más visual, y para ello, activaremos el teclado virtual pulsando en la tecla Keyboard de nuestra calculadora. Dicho teclado, presenta varias pestañas: mth, abc, cad y 2D, nosotros seleccionaremos la 2D, la cual sirve para cálculos cómo su nombre indica, con formato en 2D.

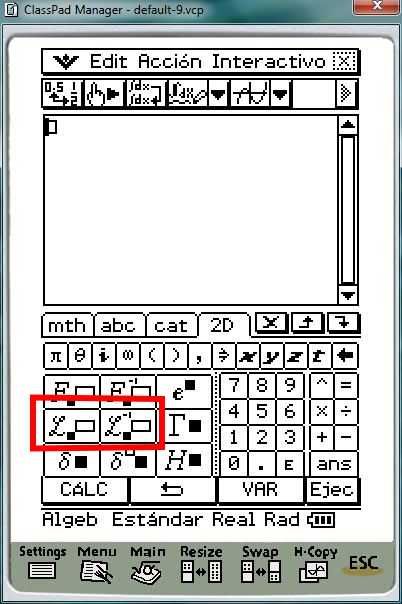
Y en dicha pestaña, abajo, tenemos las opciones: CÁLC, ADV y VAR, en nuestro caso, escogeremos ADV (Avanzado):

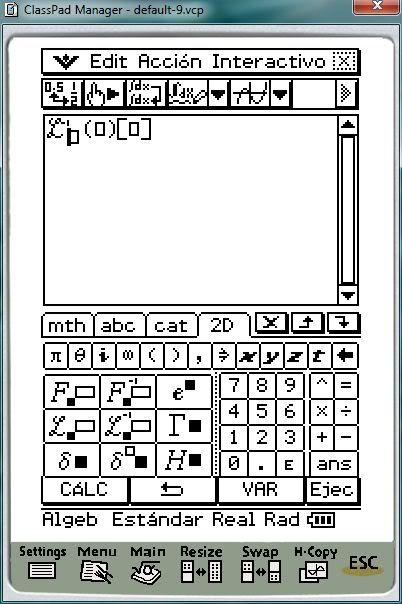
Donde podemos comprobar que existen las dos herramientas que necesitamos, la Transformada (L) y Antitransformada (L^-1) de Laplace. Primero expondremos el uso de la Transformada de laplace.

Para ello, pulsamos sobre su icono, L:

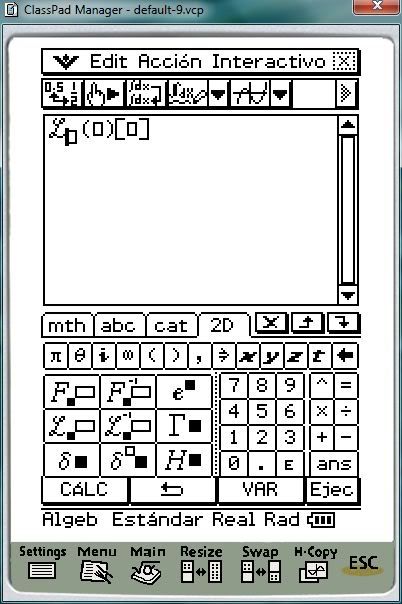
Y en pantalla se nos muestra la estructura de dicha función, dónde en el cuadrado inferior deberemos definir la variable de la función a modelar. Es decir, si tenemos la siguiente función:

f(x) = x²

La variable de la función a transformar es la x. En el cuadrado que está entre paréntesis deberemos poner la función a transformar, siguiendo con el ejemplo anterior, sería: x².

Y por último, el cuadrado que está entre corchetes, es para definir la variable de la transformada que generalmente se denomina por la letra s, pero podemos poner cualquiera.

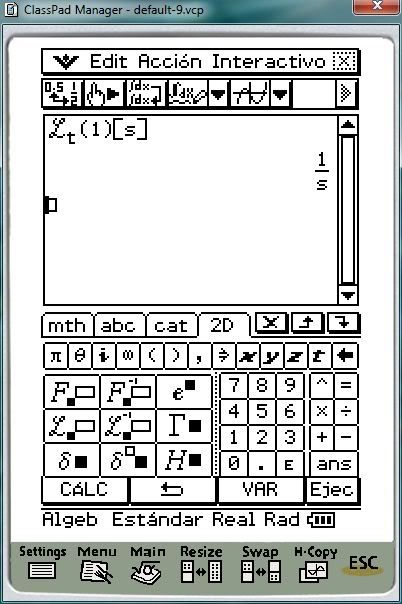
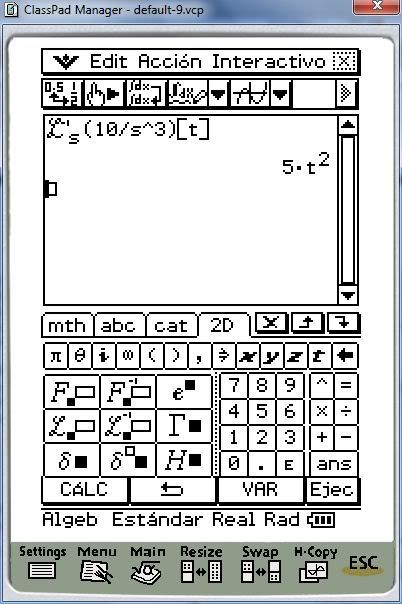
Una vez entendido cómo se debe declarar la función de Transformada de Laplace, pasaremos a realizar un ejemplo sencillo, la transformada de una constante:

Podemos comprobar, que la respuesta es satisfactoria. Para la Antitransformada de Laplace, se trabaja de forma similar, la estructura de dicha función es la que se muestra en la siguiente imagen:

En el cuadrado inferior deberemos definir la variable de la función modelada por Laplace. Es decir, si tenemos la siguiente función modelada por Laplace:

f(s) = 1/s

La variable de la función para antitransformar es la s. En el cuadrado que está entre paréntesis deberemos poner la función a antitransformar, siguiendo con el ejemplo anterior, sería: 1/s.

Y por último, el cuadrado que está entre corchetes, es para definir la variable de la antitransformada, generalmente suele ser t o x, pero se puede emplear cualquiera.

Al igual que hicimos con la transformada, pasaremos a resolver un ejemplo:

Dónde podemos comprobar que el resultado obtenido es satisfactorio.

---

Este ha sido una breve introducción a cómo transformar y antitransformar funciones en Laplace, por supuesto, en el manual de la calculadora se pueden ampliar los conocimientos y manejo de ambas funciones ya que no sólo se limita a calcular funciones concretas, sino que podemos emplear dichas funciones para resolver ecuaciones diferenciales, aunque la metodología a seguir, es similar a la expuesta en este capítulo.

Anunciar que en el manual nos hacen saber que en la ClassPad 330 no es posible obtener la Transformada de las siguientes funciones:

tan(x)	..sin-1(x)	..cos-1(x)	..tan-1(x)	..tanh(x)	..sinh-1(x)	..cosh-1(x)
tanh-1(x)	..log(x)	..ln(x)	..1/x	..abs(x)	..gamma(x)

Para concluir, este capítulo se ha realizado usando el ClassPad Manager v3 y comprobado por la ClassPad 330.