Maxima es un programa muy útil para álgebra computacional y cálculos simbólicos, aparte, dispone de multitud de funciones incorporadas, concretamente, la que trataremos en este capítulo es: Transformada de Laplace.
Aclarar, que este capítulo se ha basado en el entorno gráfico wxMaxima, pero la estructura y empleo de las funciones aquí expuestas son similares para cualquier entorno que se use.
La estructura de las funciones que vamos analizar es la que se muestra a continuación:
| Maxima: Transformada y Antitransformada de Laplace. | |
| laplace (fun, variable fun, variable Laplace) | Transformada de Laplace. |
| ilt (fun. Laplace, variable Laplace, variable temp) | Antitransformada de Laplace. |
Los argumentos que podemos pasar a la función expuesta anteriormente, son:
- fun: Función a transformar a Laplace.
- variable fun: Variable de la función a transformar.
- variable Laplace: Variable de la función transformada de Laplace.
- fun. Laplace: Función de Laplace.
- variable temp: Variable de la antitransformada de Laplace.
Una vez entendida las funciones que este programa nos pone a nuestra disposición, vamos a realizar algunos ejemplos para ver su funcionamiento.
Empezamos con la Transformada de Laplace, vamos a emplearla con la siguiente función:
f(x) = x·sin (a·x), ...a ≠ 0
Identificando las partes de la función a transformar para emplear la herramienta de la transformada:
· fun ≡ f(x)
· variable fun ≡ x
· variable Laplace ≡ Normalmente se suele denotar por la letra s, pero puede ser cualquiera.
Llegados a este punto, escribimos la función en Maxima:
laplace(x*sin(a*x), x, s)
Dónde el programa nos da como salida la transformada de la función dada:
Ahora, vamos a mostrar cómo emplear la Antitransformada de Laplace, la metodología de trabajo es igual que la función anteriormente mostrada. Como ejemplo, usaremos la obtenida por el ejercicio anterior:
Identificando las partes de la función para antitransformar:
· fun. Laplace ≡ F(s)
· variable Laplace ≡ s
· variable temp ≡ Normalmente se suele denotar por la letra t, pero puede ser cualquiera.
Llegados a este punto, escribimos la función en Maxima:
ilt((2*a*s)/(s^2+a^2)^2, s, x)
Maxima, nos pregunta por el valor del parámetro a, si es cero o no, esto es así ya que la antitransformada cambia dependiendo de dicho valor, en nuestro caso, es distinto de cero como se definió al principio.
Is a zero or nonzero? nonzero;
Y el resultado es la antitransformada de Laplace:
Como se ha podido comprobar, ambas funciones para trabajar con la herramienta de Laplace son bastantes sencillas y útiles, para profundizar más sobre ellas, se recomienda visitar la ayuda que el propio programa incorpora.

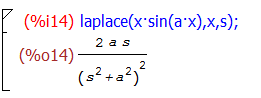





0 comentarios:
Publicar un comentario