Problema1: Laplace

Ej1. Obtenga la transformada de Laplace de la siguiente función.

f(t) = a

Siendo a una constante distinta de cero.


Para resolver este problema utilizamos la propia definición de Transformada de Laplace:

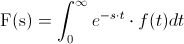
Y simplemente, debemos resolver dicha integral:

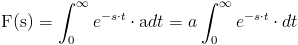
Realizamos el siguiente cambio de variable:

· x = -s·t
· dx = -s·dt

Para resolver de forma fácil la integral propuesta:

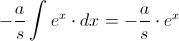
Deshacemos el cambio de variable:

· x = -s·t

Para obtener su valor:

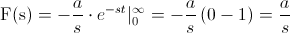
Por lo tanto, la Transformada de Laplace de la función f(t) = a, para a ≠ 0, es F(s) = a/s para s > 0.