En este capítulo se mostrará cómo es posible resolver ecuaciones de forma fácil mediante la calculadora Casio ClassPad 330.
Para tal fin, podemos usar la función solve que viene incorporada en la propia calculadora, pero en este caso, vamos a emplear el método 2D.
Arrancamos la calculadora y pulsamos sobre Principal:
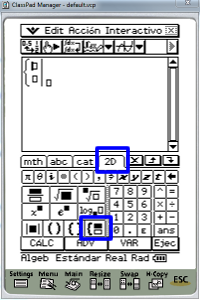
Activamos el teclado mediante la tecla Keyboard y pulsamos sobre la pestaña 2D, la herramienta que nos permitirá resolver un sistema de ecuaciones es la que se muestra en la siguiente imagen:
Como podemos observar, en la pantalla principal se habilita las propiedades de la función, para emplearla, vamos a resolver el sistema de ecuaciones siguiente cómo ejemplo:
| 2x + 4y = 2
| x - y = 3
Es un sistema de dos ecuaciones con dos incógnitas, ponemos cada ecuación en una de las filas y definimos las variables con las cuales queremos resolver dicho sistema
Y lo que nos queda, es pulsar sobre la tecla Exe o sobre la opción Ejec para obtener la solución al sistema de ecuaciones dado:
Por lo tanto, la solución es:
· x = 7/3.
· y = -2/3.
Si tenemos un sistema de ecuaciones más amplio, seguiremos los pasos aquí explicados donde se pueden insertar dos ecuaciones, para insertar más, debemos pulsar sobre la opción CÁLC, y para insertar otra ecuación, debemos pulsar sobre la opción que se muestra en la siguiente imagen:
Como se puede observar, se ha incluido una tercera ecuación, y así, hasta las que se desee.
A partir de este punto, resolver cualquier sistema de ecuaciones es fácil siguiendo las anotaciones que en este capítulo se exponen.
Para profundizar más sobre este método para resolver sistemas de ecuaciones, se recomienda que se visite el manual de la propia calculadora.








7 comentarios:
que buenas explicaciones les dejo uan pagina de sugerencia
visintela
http://calculadoras.com.mx/casio-impresoras/casio-hr-150tm.php
q bien gracias por la explicacion
Excelente explicacion. Muchas Gracias por compartir.
muchas gracias, es muy practico,ahora mas rapido sera las formas pa resolver las ecuaciones.
Excelente tutorial! pero una pregunta como hago para resolver un sistemas de ecuaciones con numero complejos? me explico mejor tengo un sistema de ecuaciones donde tengo argumentos y angulos en forma polar! pero no se como colocar los datos en la calculadora y q ella me genere un resultado! espero respuesta por favor! es para un parcial de circuitos!
Buenas:
Para trabajar en complejos de la forma:
· a + j·b
Donde:
· j = Parte imaginaria
Es igual que trabajar con un sistema no complejo, es decir, te vas a la pestaña 2D, montas su sistemas de ecuaciones (En la ClassPad, para indicar la parte imaginaria es la letra i), y simplemente te tienes que asegurar que tu calculadora está trabajando en modo complejo.
Abajo, en la pantalla táctil, a la izquierda de la batería, es el lugar de Rad, Grad etc, a la izquierda de este, debes asegurarte de que ponga: Cplx.
Y ya te dará los resultados.
Si tienes los datos en forma polar, desde la versión 3.06, puedes usar la siguiente función para pasarlo a la forma que antes te he puesto, la función es:
· compToRect()
Un ejemplo, tenemos el siguiente dato complejo en polar:
25<78
Donde:
· Argumento: 25
· Ángulo: 78
En la calculadora lo escribiremos de la siguiente forma:
· 1. Nos dirigimos a la pestaña de mth.
· 2. Seleccionamos OPTN
· 3. Y ahí está la función polar (es algo parecido a un ángulo)
Pues, pulsamos e introducimos nuestro dato:
· <(25, 78)
Si pulsamos EXE, nos lo mostrará por pantalla, ahora, vamos a convertirlo en coordenadas rectangulares, simplemente, con la función que he mencionado anteriormente:
· compToRect(ans)
Donde ans es nuestro número en polar, si pulsamos EXE nos devolverá nuestro número en coordenadas cartesianas.
Un saludo y gracias por tu comentario.
Hola, hay como resolver sistemas de ecuaciones diferenciales?
Gracias
Publicar un comentario