Problema10: Laplace EDO

Ej10. Resuelva la siguiente ecuación diferencial.

Resolveremos el problema empleando la herramienta de transformada y antitransformada de Laplace.

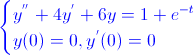
L{y''} + 4L{y} + 6L{y} = L{1} + L{e^-t}

Mirando en las tablas y propiedades que dispone Aqueronte, podemos escribir su transformada:

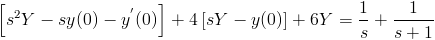
Agrupo:

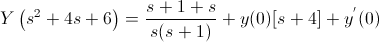
Empleo el dato de valor inicial:

· y(0) = 0
· y'(0) = 0

Por lo tanto:

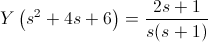
Despejo para obtener la Transformada de Laplace:

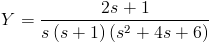
En estos momentos, tenemos recorrer el camino contrario, ya que hemos obtenido la transformada de la función con las condiciones dadas, debemos hallar la antitransformada para resolver el problema.

Descomponemos el denominador en fracciones:

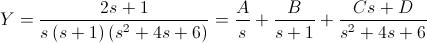
Operamos:

2s + 1 = A(s+1)(s²+4s+6) + Bs(s²+4s+6) + Cs²(s+1) + Ds(s+1)

Opero:

2s + 1 = As³ + 5As² + 10As + 6A + Bs³ + 4Bs² + 6Bs + Cs³ + Cs² + Ds² + Ds

Agrupamos por términos:

· s³: A+B+C = 0
· s²: 5A+4B+C+D = 0
· s¹: 10A+6B+D = 2
· s⁰: 6A = 1

Resolvemos el sistema formado por cuatro ecuaciones con cuatro incógnitas, dando como resultado:

· A = 1/6
· B = 1/3
· C = -1/2
· D = -5/3

Por lo tanto, la ecuación nos queda de la siguiente manera:

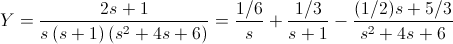
La antitransformada que debemos obtener es la siguiente:

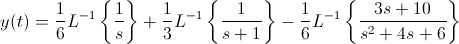
En estos momentos, estamos en disposición de identificar algunos miembros de la función acorde a las dadas en las tablas.

• Primer Miembro: Transformada de Laplace de la función: f(t) = 1

L{1} = 1/s

• Segundo Miembro: Transformada de Laplace de la función: f(t) = e^at

L{e^at} = 1/(s-a)

Siendo:

· a = -1.

Adaptamos la función para obtener las antitransformadas planteadas teniendo en cuenta que la antitransformada de los dos primeros miembros es inmediata:

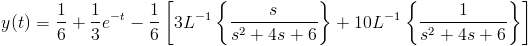
El denominador de los dos últimos miembros presentan la siguiente estructura:

a·s² + b·s + c

Identificamos los elementos:

· a = 1
· b = 4
· c = 6

Podemos completar cuadrados si la agrupamos de la siguiente forma:

a·(s+k)² + h²

Siendo:

·

·

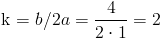
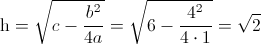
Por lo tanto:

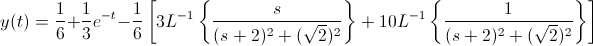
Miramos las tablas y buscamos una transformada que presente similitud a la obtenida, en nuestro caso, la que nos interesa es la que se muestra a continuación.

• Tercer Miembro: Transformada de Laplace de la función: f(t) = e^b·t·cos(k·t)

L{e^b·t·cos(k·t)} = (s-b)/[(s-b)²+k²]

Siendo:

· b = -2.
· k = √2.

• Cuarto Miembro: Transformada de Laplace de la función: f(t) = e^b·t·sin(k·t)

L{e^b·t·sin(k·t)} = k/[(s-b)²+k²]

Siendo:

· b = -2.
· k = √2.

Debemos adaptar la función y expandimos el primer miembro, para que se asemeje a la que queremos obtener:

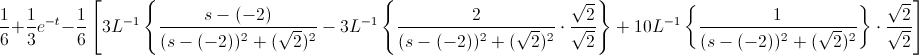
En estos momentos, la antitransformada de los miembros, son inmediatas, y por lo tanto, la solución a este problema es:

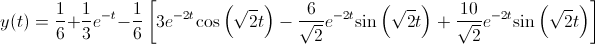
Por lo tanto, la solución a este problema es:

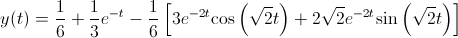
Como se puede observar, el resolver ecuaciones diferenciales mediante la herramienta de Laplace se hace más amena que por la vía convencional.