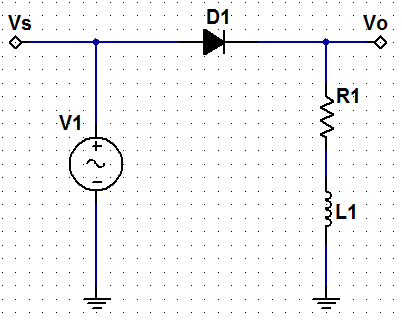
En esta ficha vamos a estudiar el Rectificador de Media Onda: Carga Resistiva-Inductiva. Este circuito consiste en una fuente alterna de entrada, un conmutador (en este caso emplearemos un diodo), una resistencia y un inductor, se suelen asociar al apartado de rectificadores no controlados.
Los objetivos principales que buscamos son:
- Análisis de circuitos de este tipo.
- Obtención de expresiones matemáticas finales que definan este tipo de circuitos.
- Obtención de gráficas de tensión e intensidad (si se requieren) para posterior análisis.
Al estar presente un diodo, podemos escoger entre cualquiera de los modelos: Modelo ideal, 1ª Aproximación o 2ª Aproximación. En la mayoría de los casos (y más en el ámbito de la electrónica de potencia, es aconsejable emplear los modelos ideales ya que el error que se cometerá será muy bajo).
Pero en nuestro caso, al ser éste una ficha de estudio, vamos a emplear la 2ªAproximación y de ésta obtendremos las ecuaciones matemáticas de los modelos inferiores. ¡Manos a la obra! Estudiaremos ambos semiciclos por separado.
· Semiciclo Positivo.
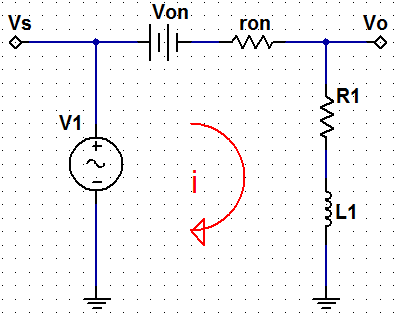
Esto quiere decir que la tensión de entrada es positiva, el diodo está en estado de conducción y el circuito equivalente (empleando la 2ª Aproximación del diodo) es el que se muestra a continuación:
Resolvemos la maya en la dirección que se muestra en la figura obteniendo la siguiente expresión (asumimos que el inductor está completamente descargado):
-V1 + i·ron + Von + i·R1 L·Di = 0
· NOTA: He utilizado el operador D = d/dt, para simplificar la nomenclatura.
Agrupamos:
i·(ron + R1) + L·Di = V1 - Von
Si tenemos en cuenta que la mayoría de veces la fuente de entrada es del tipo sinusoidal cómo:
· V1 = Vm·sen(wt), siendo Vm la amplitud en RMS (valor eficaz).
Pues tenemos la siguiente solución:
i·(ron + R1) + L·Di = Vm·sen(wt) - Von
Emplearemos la Transformada de Laplace para resolver la anterior expresión:
Agrupamos en torno a la variable intensidad teniendo en cuenta que la bobina estaba completamente descargada: i(0) = 0:
Despejamos, acondicionamos y descomponemos en fracciones parciales [Ecuación 1]:
Operamos:
A(s2+w2)[s-(-(ron + R1)/L)] + Bs3 + Bsw2 + Cs2[s-(-(ron + R1)/L)] + Ds[s-(-(ron + R1)/L)]
Descomponemos:
As3 + As2(ron + R1)/L + Asw2 + Aw2(ron + R1)/L + Bs3 + Bsw2 + Cs3 + Cs2(ron + R1)/L + Ds2 + Ds(ron + R1)/L
Agrupamos por términos:
· s3: A + B + C = 0
· s2: A(ron + R1)/L + C(ron + R1)/L + D = - Von/L
· s1: Aw2 + Bw2 + D(ron + R1)/L = wVm/L
· s0: Aw2(ron + R1)/L = - w2Von/L
Resolvemos el sistema formado por cuatro ecuaciones con cuatro incógnitas, dando como resultado:
· A = -Von/(ron+R1)
· B = [Von·R12 + (w·L·Vm+2ronVon)R1 + L2·Von·w2 + ron·Vm·w·L + ron2·Von]/[R13 + 3ron·R12 + (w2·L2 + 3ron2)R1 + w2·ron·L2 + ron3]
· C = - w·L·Vm/[R12 + 2ron·R1 + w2·L2 + ron2]
· D = [w·R1·Vm + w·ron·Vm]/[R12 + 2ron·R1 + w2·L2 + ron2]
Ahora viene la parte más tediosa y es el sustituir el valor de las variables obtenidas en la expresión de la intensidad [Ecuación 1], como podéis observar, son bastantes valores los que tenemos que operar.
Dicha tarea no la voy a realizar aquí ya que no tendría demasiado sentido y la expresión obtenida no sería muy legible que digamos, entonces ¿por qué hemos elegido esta forma de resolver el circuito (mediante Laplace)? Pues es simple, (a parte de ser otra forma de operar), es porque, mediante tablas es bastante fácil de obtener el resultado final.
Y eso es justamente lo que vamos a hacer en este punto, vamos a identificar mediante la antitransformada, que tipo de función es la que corresponde e iremos obteniendo la solución a aquellas expresiones que sean inmediatas y acondicionando aquellas para su posterior antitransformada.
Por lo tanto, volviendo a la [Ecuación 1] vemos que las expresiones corresponden a la antitransformada siguientes:
• Primer Miembro (A): Transformada de Laplace de la función: f(t) = 1
L{1} = 1/s
• Segundo Miembro (B): Transformada de Laplace de la función: f(t) = eat
L{eat} = 1/(s-a)
Siendo:
· a = -(ron + R1)/L .
• Tercer Miembro (C): Transformada de Laplace de la función: f(t) = cos(k·t)
L{cos(k·t)} = s/(s2+k2)
Siendo:
· k = w.
• Cuarto Miembro (D): Transformada de Laplace de la función: f(t) = sin(k·t)
L{sin(k·t)} = k/(s2+k2)
Siendo:
· k = w.
Una vez identificadas las antitransformadas, obtenemos (por fin) el valor de la intensidad del circuito:
¿Es grande la expresión? (-Risas-) Pues sí, pero no hay que asustarse todavía, ahora vamos a simplificarla:
· (ron + R1)2 = R12 + 2ronR1 + ron2
Vamos a factorizar tanto el numerador cómo el denominador del segundo y tercer miembro de la expresión de la intensidad obtenida empleando el resultado anterior, como ejemplo, muestro cómo se hace para el segundo miembro:
Simplificando, obtenemos:
Von/(ron + R1)
Teniendo en cuenta la anterior relación, la cosa va cambiando a mejor:
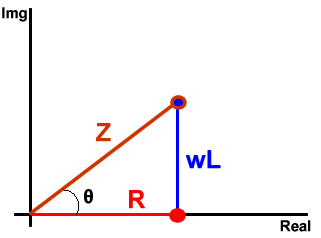
¿Ya hemos terminado? No, aún queda por simplificar un poco más (no te desanimes). Ahora es el momento de aplicar los conocimientos electrónicos, concretamente el comportamiento de un inductor en alterna. La manera más simple es gráficamente:
Dónde:
· Z = [(ron + R1)2 + (wL)2]1/2
· sinθ = wL/Z = wL/[(ron + R1)2 + (wL)2]1/2
· θ = arctg[wL/(ron + R1)]
Y por último, teniendo en cuenta la siguiente expresión trigonométrica: Podemos obtener una solución definitiva (y es la que aparece en la mayoría de textos) para la intensidad que recorre este tipo de circuitos:
Para obtener la tensión en la carga simplemente utilizaríamos la Ley de Ohm (V = I·R).
El estudio no debe concluir aquí, ya que debemos exponer (de forma clara) las condiciones de cambio de estado del diodo y así de esta manera, obtener los límites de funcionamiento.
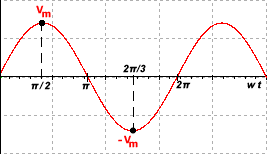
La onda de entrada (V1) debe presentar la siguiente forma (forma senoidal):
En este tipo de circuitos, al tener un elemento que almacena energía (el inductor), no tiene mucho sentido hablar del semiciclo negativo, más bien debemos obtener cuando el diodo pasa de conducción a corte y por ende, el valor de la intensidad es cero. Para ello, vamos a realizar un cambio de variable:
· wt = β
Por lo tanto, debemos resolver la siguiente expresión:
No esperéis una solución analítica ni intentéis despejar el parámetro β, para obtenerlo se necesita algún método numérico.
Habiendo realizado un análisis con la 2ªAproximación del diodo, es fácil obtener las expresiones del modelo ideal y de la 1ªAproximación. Se muestra en la siguiente tabla las expresiones para cada tipo de modelo y análisis para el circuito rectificador de media onda no controlado con carga resistiva-inductiva:
| Modelo Ideal | 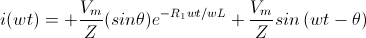 |
| Modelo 1ªAproximación | 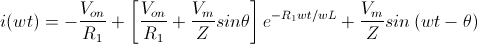 |
| Modelo 2ªAproximación | 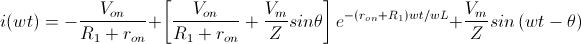 |
Dónde:
| Modelo Ideal | · Z = [R12 + (wL)2]1/2 · sinθ = wL/Z = wL/[R12 + (wL)2]1/2 · θ = arctg[wL/R1] · τ = L/R1 |
| Modelo 1ªAproximación | · Z = [R12 + (wL)2]1/2 · sinθ = wL/Z = wL/[R12 + (wL)2]1/2 · θ = arctg[wL/R1] · τ = L/R1 |
| Modelo 2ªAproximación | · Z = [(ron + R1)2 + (wL)2]1/2 · sinθ = wL/Z = wL/[(ron + R1)2 + (wL)2]1/2 · θ = arctg[wL/(ron + R1)] · τ = L/(ron + R1) |
Llegados a este punto, hemos identificado, analizado y obtenido las expresiones matemáticas necesarias para este tipo de circuitos, ahora, nos falta aportar, de manera gráfica, el resultado en forma de tensión (entrada contra salida).
Para este tipo de circuitos: Rectificador No Controlado Media Onda: Carga Resistiva-Inductiva, las gráficas de tensión son las que se muestran a continuación:
| Tensión de entrada: Vs |
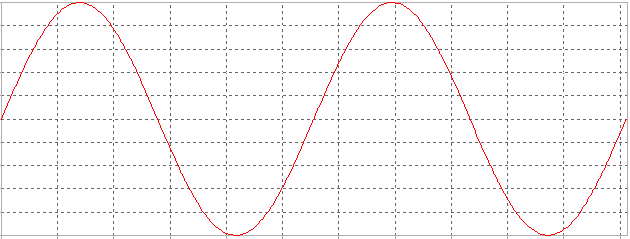 |
| Tensión de salida: Vo |
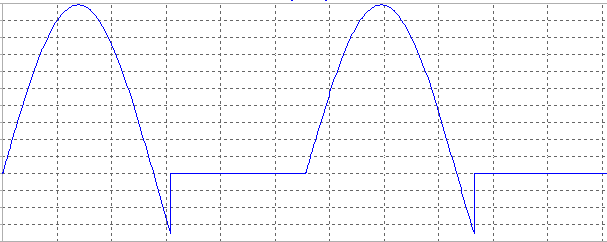 |
Como se puede observar, el circuito sigue en parte a la tensión de entrada incluso en el semiciclo negativo hasta llegado un valor (nuestro β), esto es así por la influencia del inductor.
Por último, se facilita scripts (o programas) para distintas plataformas dónde poder obtener los cálculos necesarios para este tipo de circuito de manera automática:
| --En Construcción-- |
|---|
| --- |
| --- |
También os podéis descargar el circuito estudiado en esta ficha para que lo simuléis vosotros mismos:
 |  | Rectificador No Controlado Media Onda: Carga Resistiva-Inductiva |
 |  | Rectificador No Controlado Media Onda: Carga Resistiva-Inductiva |
Para terminar, haremos un par de reflexiones, la primera, entorno a los cálculos matemáticos: Quizás, al ver la longitud de las expresiones (y la cantidad de parámetros) uno tiende a pensar que el cálculo es difícil, pero no es cierto, si se tiene un uso (preferiblemente medio) de la Transformada de Laplace, realizar éstos cálculos no es para nada dificultoso y además, es bastante inmediato el obtener la solución mediante las tablas. Aparte, no necesitamos emplear los conocimientos de cálculos en alterna (operar con números complejos).
Por otro lado, entorno a la electrónica, este tipo de circuitos nos muestra que la intensidad no se anula (y por lo tanto, el diodo no entra en corte) en el semiciclo negativo cómo podíamos pensar, esto es así por la influencia del inductor, que se va cargando (de energía) y obliga a que el diodo corte más tarde.

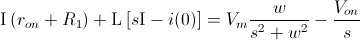
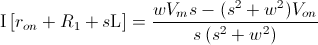
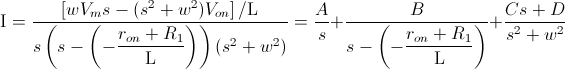
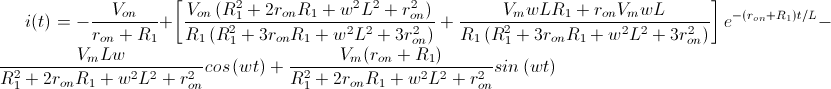
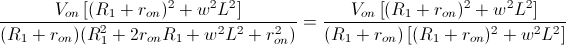
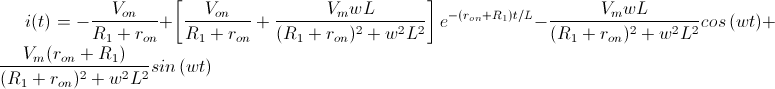
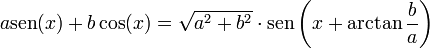
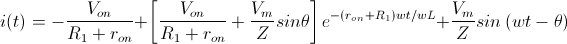
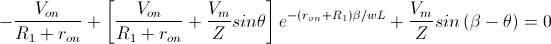




1 comentarios:
Excelente desarrollo... Felicitaciones
Publicar un comentario