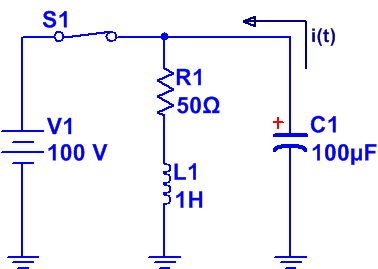
Ej2. El interruptor ha permanecido cerrado durante un largo período de tiempo, en el instante t = 0, se abre el interruptor.
Obtener la evolución de i(t).
Vamos a analizar el circuito dado por el enunciado del problema teniendo en cuenta la posición del interruptor.
· t < 0: S1 Cerrado.
El enunciado nos advierte que en esta posición ha estado durante un largo período de tiempo, por lo que el circuito que vamos a tener estará, solo, en régimen permanente.
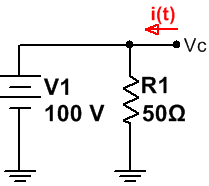
El condensador se comportará como un circuito abierto y el inductor como un corto circuito, el circuito que tendremos es el siguiente:
El valor de la intensidad que nos piden en el enunciado del problema, es fácil obtenerla:
· ip = 0 A.
Aparte, necesitaremos saber si los componentes (ya sea el condensador o el inductor) se van a cargar para el siguiente cambio del interruptor:
· VCp = V1 = 100 V
· iLp = V1/R1 = 100/50 = 2 A
Por lo tanto, ambos elementos presentarán una carga inicial justo en el momento que el interruptor cambie de posición.
Abrimos el interruptor y analizamos el comportamiento.
· t = 0: S1 Abierto.
Cuando tenemos elementos cargados, como en este caso, podemos dibujar el circuito equivalente en función de dichos elementos:
· Condensador: Un condensador sin polaridad y de la misma capacidad pero sin ninguna carga inicial, con una fuente de tensión lineal en serie de valor y polaridad a la carga inicial del condensador.
· Inductor: Un inductor del mismo valor, con una fuente de corriente lineal en paralelo de valor y polaridad a la carga inicial del inductor.
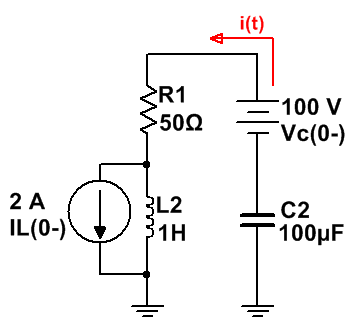
Por lo tanto, teniendo en cuenta dichas premisas, el circuito que tenemos es el siguiente:
· NOTA: Tanto el condensador C2 cómo el inductor L2 es de la misma capacidad e inductancia respectivamente, que el condensador inicial del circuito (C1) y la inductancia inicial del circuito (L1), pero no tiene la misma polaridad, aparte, el condensador no tiene ninguna carga inicial, es por ello, que al no ser el mismo (ya que hemos empleado las condiciones de equivalencia para cuando existen elementos cargados), se ha nombrado cómo: C2 y L2.
En estas condiciones, tenemos dos comportamiento en el circuito, por un lado: El régimen transitorio (in) y por el otro: El régimen permanente (ip). La solución general será del tipo:
· i(0+) = ip + in
Así que vamos a obtener los dos por separado.
· Régimen Permanente:
Este caso, el interruptor S1 ha estado abierto durante un largo período de tiempo, tanto el condensador cómo el inductor se descargarán.
Por lo que, los datos que tendremos son:
· ip = 0 A.
Y evidentemente, la carga de ambos elementos serán nulas ya que se descargarán:
· VCp = 0 V
· iLp = 0 A
· Régimen Transitorio:
Tanto el condensador cómo el inductor se irán descargando, realizamos el análisis mediante LVK:
· [Ec1] VR1 + VL2 + VC2 = 100
Sustituimos por sus expresiones en [Ec1]:
· in·R1+ L2·Din + (1/DC2)·in = 100
Multiplicamos por el operador D y dividimos por L2:
· [Ec2] D2 in + Din·(R1/L2) + (1/L2·C2)·in = 0
Ya tenemos nuestra ecuación diferencial de 2º Orden Homogénea, que sabemos que debe ser del tipo:
· s2 + 2α·s + w20 = 0
Y en este caso, los parámetros α y w0 son:
· Factor de amortiguamiento ≡ α = R1/(2·L2) = 50/(2·1) = 25
· Frecuencia natural ≡ w0 = √[ (1/L2·C2)] = √[ (1/1·100·10-6)] = √10000 = 100 rad/s
Y teniendo el valor de estos dos parámetros, podemos determinar cual es el comportamiento de nuestro circuito. En nuestro caso:
· α < w0
Al ser la frecuencia natural mayor que el factor de amortiguamiento, el comportamiento de nuestro circuito es: Respuesta Subamortiguada, cuya solución a la respuesta homogénea es:
· in(t) = e-α·t·[k1·cos(wd·t) + k2·sin(wd·t)]
Dónde:
· Frecuencia natural amortiguada ≡ wd = (w20 - α2)1/2 = (1002 - 252)1/2 ≈ 96.824584 rad/s
Por lo tanto, la solución completa es, la compuesta por la respuesta permanente más la respuesta transitoria:
· i(t) = ip + in = 0 + e-25·t·[k1·cos(96.824584·t) + k2·sin(96.824584·t)]
Simplificamos:
· i(t) = e-25·t·[k1·cos(96.824584·t) + k2·sin(96.824584·t)]
Ya tenemos la estructura de cómo será la evolución de la intensidad al abrirse el interruptor de nuestro circuito. Nos falta obtener los valores de los parámetros.
Para ello, vamos a aplicar las condiciones iniciales de los componentes que forman nuestro circuito.
· Inductor:
La corriente no puede cambiar bruscamente en un instante concreto. El inductor de nuestro circuito, presenta la siguiente carga de corriente inicial:
· iL(0-) = 2 A
En el instante t = 0:
· iL(0-) = iL(0+)
Por lo tanto:
· 2 = e-25·0·[k1·cos(96.824584·0) + k2·sin(96.824584·0)] = k1
Despejamos:
· k1 = 2
Ya tenemos el valor del primer parámetro, ahora vamos a por el del segundo parámetro, para ello, analizamos las condiciones iniciales del siguiente componente, en nuestro caso, las condiciones iniciales del condensador.
· Condensador:
La tensión no puede cambiar bruscamente en un instante concreto. El condensador de nuestro circuito, presenta una carga de tensión inicial:
· VC1(0-) = 100 V.
Hay varias maneras de abordar este aspecto, la más directa es mediante la expresión matemática que describe el comportamiento de la tensión del condensador, pero quizás, sea la más compleja (aún así, se expone más abajo cómo obtenerla mediante el uso de wxMaxima), hay que realizar un par de integrales por partes, no son difíciles, pero hay que hacerlas :)
En nuestro caso, vamos a ir por el camino más sencillo, y en este caso es volver a realizar un análisis LVK al nuestro circuito, obteniendo el mismo resultado que anteriormente en [Ec1]:
· [Ec1] VR1 + VL2 + VC2 = 100
Teniendo en cuenta la condición del condensador:
· VC2(0-) = VC2(0+) = 0
El condensador C2 no presentaba ninguna carga inicial, por lo que en el instante t = 0, para ser consistente con las premisas de éste elemento, debe tener el mismo valor. Por lo tanto, sustituimos en [Ec1]:
· VR1 + VL2 = 100
Sustituimos por las expresiones matemáticas que describen el comportamiento de la tensión de los elementos que conforman la expresión anterior:
· [Ec3] i(t)·R1+ L2·Di(t) = 100
La estructura de la corriente que circula por el circuito la hemos calculado anteriormente, siendo:
· i(t) = e-25·t·[2·cos(96.824584·t) + k2·sin(96.824584·t)]
Obtenemos su derivada:
· Di(t) = -25·e-25·t·[2·cos(96.824584·t) + k2·sin(96.824584·t)] + e-25·t·[-193.649168·cos(96.824584·t) + 96.824584·k2·sin(96.824584·t)]
Y en el instante t = 0, tanto la corriente como su derivada son:
· i(0) = 2
· Di(0) = -50 + 96.824584·k2
Ahora, sustituimos en [Ec3]:
· 2·R1+ L2·(-50 + 96.824584·k2) = 100
Sustituimos los valores tanto del resistor cómo del inductor y despejamos el parámetro que nos interesa obtener:
· k2 ≈ 0.516398
Ya hemos obtenido ambos parámetros, por lo que, una expresión para la corriente del circuito es:
· i(t) = e-25·t·[2·cos(96.824584·t) + 0.516398·sin(96.824584·t)], t ≥ 0
Por lo tanto, en modo resumen, una expresión para la evolución de la corriente, dadas las condiciones que nos expone el enunciado del problema, es:
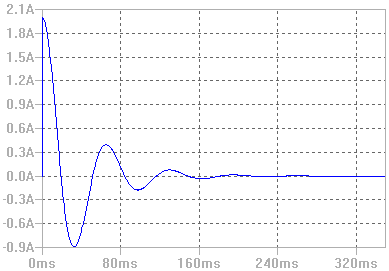
Cuya representación gráfica es:
Aquí explicaremos cómo obtener el parámetro k2 mediante la propia definición de la tensión del condensador, la cual es:
· VC(t) = (1/C1D)·iC(t)
Sabemos, ya que se ha obtenido anteriormente, que la estructura de la corriente es:
· i(t) = e-25·t·[2·cos(96.824584·t) + k2·sin(96.824584·t)]
La condición que hay que tener en cuenta del condensador es que no puede cambiar bruscamente su tensión en un momento determinado.
· VC1(0-) = VC1(0+) = 100 V
Muy bien, ya tenemos todo lo necesario para obtener nuestro parámetro k2, pero antes de eso, hay que tener en cuenta que la intensidad del condensador es contraria a la intensidad obtenida:
· iC(t) = - i(t) = - e-25·t·[2·cos(96.824584·t) + k2·sin(96.824584·t)]
Vamos a obtener el parámetro requerido mediante wxMaxima. Primero, introducimos el valor de la corriente del condensador:
>> i_C: -(%e^(-25*t))*(2*cos(96.824584*t) + k_2*sin(96.824584*t));
Obtenemos la tensión del condensador:
>> V_C: (1/C)*integrate(i_C, t);
Y aplicamos la condición del condensador:
>> equ1: 100 = V_C;
Ahora, sustituimos valores y evaluamos dicha expresión en el instante t = 0:
>> equ2: subst([t = 0, C = 100*10^(-6)], equ1);
Ya solo nos falta resolver para nuestro parámetro:
>> solve(equ2, k_2);
Cuyo resultado es:
>> k_2 = 0.5163977845516
Como podemos ver y comprobar, ambos métodos coinciden.
Os dejo una simulación realizada en LTSpice:
| Problema 2: Transitorios de 2º Orden | |||||||||
|

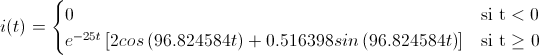








0 comentarios:
Publicar un comentario