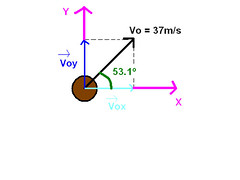
Problema 2. Un bateador golpea una bola de modo que ésta adquiere una rapidez inicial de v0 = 37m/s con un ángulo inicial α0 = 53.1º en un lugar donde g = 9.8 m/s2. Calcule:
a) La posición de la bola, la magnitud y dirección de su velocidad cuando han transcurrido 2 segundos.
b) Cuándo la pelota alcanza su punto más alto y su altura en ese instante.
c) El alcance horizontal desde que se lanzó hasta que la bola cae al suelo.
En el problema no nos habla de que actúa fuerzas externas, como la del aire, por lo tanto, despreciamos dichas fuerzas.
El movimiento que describe la bola es de una parábola, eso quiere decir, que tenemos que calcular sus magnitudes tanto en el eje de referencia “Y” como en el “X”.
Por lo tanto, lo primero que hay que hacer, es fijar los ejes de referencias. En este caso, el instante inicial, lo he escogido justo en el momento de que la bola es lanzada, eso conlleva a que su posición inicial, tanto en el eje “X” como en el “Y” sean cero.
El eje de referencia “Y” lo he escogido hacia arriba, y el eje “X” hacia la derecha.
Figura 1.
En el instante inicial, como se puede observar en la Figura 1, la bola tiene una velocidad inicial de 37m/s, esta velocidad, tendrá sus proyecciones tanto en el eje “X” como en el eje “Y”.
Obtenemos el valor de sus proyecciones:
Eje X: Movimiento rectilíneo uniforme.
Sustituimos valores:
Eje Y: Movimiento uniformemente acelerado.
Sustituimos valores:
Hay que notar, que el signo de la fuerza gravitatoria, g, es negativo, esto es así ya que va en sentido contrario al eje de referencia “Y” que yo he fijado.
Una vez planteado el problema, se está apto para su resolución por apartados.
Apartado a)
En este apartado, nos piden la posición de la bola, la magnitud y la dirección de la velocidad en el instante de tiempo de 2 segundos.
Para ello, calculamos los datos en los distintos ejes de referencias.
Eje X: Movimiento rectilíneo uniforme.
La posición:
Sustituyo valores:
x (2) = 0 + 22.22 ·2 = 44.44m.
La velocidad:
Sustituyo valores:
vx (2) = 22.22m/s.
En este resultado, observamos que su velocidad no cambia, esto es cierto ya que en un movimiento rectilíneo uniforme, su velocidad es constante.
Eje Y: Movimiento uniformemente acelerado.
La posición:
Sustituyo valores:
La velocidad:
Sustituyo valores:
vy (2) = 29.59 + (-9.8)·2 = 9.99m
Se puede observar, que ambas velocidades, tanto en el eje “X” como en el eje “Y”, son positivas, esto indica que la bola sigue ascendiendo.
Una vez obtenido los resultados en los ejes de referencias, pasamos a obtener la magnitud de la velocidad:
Sustituimos valores:
Para calcular su dirección, calculamos el ángulo que forma con la horizontal:
Sustituimos valores y despejamos el parámetro α:
Esto quiere decir, que en el instante de 2 segundos, el vector velocidad forma un ángulo de 24.21º con el eje horizontal.
Apartado b)
Para calcular cuando la bola alcanza su punto más alto, simplemente hay que saber, que en dicho punto la velocidad de la bola es cero.
Por lo tanto debemos saber, en que instante la velocidad de la bola se hace cero.
Ya que estamos hablando de altura, en este apartado sólo es necesario el eje “Y”.
Calculamos el instante donde la pelota tiene velocidad cero.
Eje Y: Movimiento uniformemente acelerado.
La velocidad:
Sustituyo valores:
0 = 29.59 + (-9.8)·t
Despejo el parámetro t:
t ≈ 3.02s
En el instante de tiempo 3.02 segundos, la bola tiene velocidad cero.
Para calcular su altura máxima en ese instante, nos basamos de la ecuación de la posición en el eje “Y”.
Sustituimos valores:
La altura máxima es de 44.67m.
Apartado c)
Para obtener la distancia que recorre la bola, desde que se lanza hasta que cae de nuevo al suelo, debemos darnos cuenta que en el eje “Y” su posición es cero.
Por lo tanto, primero debemos saber cuanto tiempo tarda la bola en caer, para ello nos basamos en la ecuación de la posición del eje “Y”:
Eje Y: Movimiento uniformemente acelerado.
Sustituimos valores:
Reordenamos la ecuación:
t·(4.9·t – 29.59) = 0
Al ser una ecuación cuadrática, obtenemos dos valores:
t1 = 0s
t2 ≈ 6.04s
El instante 0 segundos, es al principio del todo, cuando la bola está justo en el momento inicial.
Por lo tanto, la solución válida para este apartado, es el instante de 6.04 segundos aproximadamente. Éste es el instante que tarda la bola en caer.
Eso quiere decir, que para saber cuanto ha recorrido, sólo basta recurrir a la ecuación de la posición del eje “X”:
Eje X: Movimiento rectilíneo uniforme.
Sustituyo valores:
x (6.04) = 0 + 22.22 ·6.04 ≈ 134.21m
0 comentarios:
Publicar un comentario