Ej17. El número de clientes que entran en un banco en una hora es una variable aleatoria de Poisson y P(X = 0) = 0.05.
Calcula la media y la varianza de X.
Para la distribución de Poisson, la media se obtiene de la siguiente expresión:
μx = E(X) = λ
Para hallar el parámetro λ, debemos operar en la expresión de la distribución de Poisson:
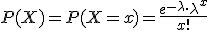
Nos dan como dato: P(X = 0) = 0.05, por lo tanto:
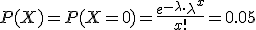
Se opera tomando logaritmos neperianos:
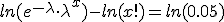
Se sigue las propiedades de los logaritmos:
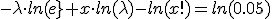
Se simplifica, obteniendo el valor del parámetro λ:
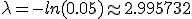
Por lo tanto, la media es:
μx = E(X) = λ = 2.995732
La varianza en las distribuciones de Poisson es igual al valor de la media:
σx2 = E[(X - μx)2 = λ
Por lo tanto:
σx2 = E[(X - μx)2 = λ = 2.995732





8 comentarios:
¿cual es la probabilidad de que, en una hora cualquiera, entren 2 y 4 clientes?
Buenas:
En este problemas ya se ha obtenido el parámetro medio:
· λ = 2.995732
Por lo tanto, ya estamos en condiciones de obtener cualquier probabilidad mediante la distribución de Poisson siempre y cuando se mantenga que la escala del parámetro es de una hora, en otro caso se deberá adaptar.
Ahora bien, ¿lo que pides es que entren entre 2 y 4 clientes (ambos incluidos)?
En este caso, debemos hallar:
· P(2 ≤ X ≤ 4) = P(X=2)+P(X=3)+P(X=4)
Empleando el software R:
> sum(dpois(c(2,3,4), 2.995732))
[1] 0.6161932
En caso de que ambos límites estén excluidos:
· P(2 < X < 4) = P(X=3)
Empleando el software R:
> dpois(c(3), 2.995732)
[1] 0.2240411
Y en caso de que simplemente entren 2 y 4 clientes, hallamos las probabilidades por separado de los clientes dados:
· Para la entrada de 2 clientes:
> dpois(c(2), 2.995732)
[1] 0.2243603
· Para la entrada de 4 clientes:
> dpois(c(4), 2.995732)
[1] 0.1677918
Espero haberte ayudado y disculpa la tardanza de mi respuesta.
Un saludo y gracias por tu comentario.
Hola: Una consulta es posible obtener la media, si solo se me proporciona que X es una variable aleatoria Poisson de la que se sabe que P (X=0)=0.5?En este ejemplo no me queda claro como se obtuvo este dato:
σx2 = E[(X - μx)2 = λ = 2.995732
Me podrian explicar un poco mas por favor, en mi ejercicio me dan las sigs opciones:
a. 2.
b. -ln2.
c. No se puede calcular con estos datos.
d. Ninguna de las anteriores.
Gracias de antemano y Feliz Dia.
Buenas:
Sí se puede obtener el parámetro de Poisson con el dato que te han dado, si te das cuenta, es igual que el ejercicio resuelto pero en vez de ser el dato dado: P(X=0)=0.5 es P(X=0)=0.05.
Con respecto a la varianza, es simplemente la definición matemática de la varianza, que para las variables aleatorias discretas que sigan una distribución de Poisson, tanto la media como la varianza coinciden con el parámetro de Poisson.
Un saludo.
Hola! ¿Cómo plantearía si le pedirían el número más probable de clientes que entrarán en el banco la próxima hora? ¿Se puede hacer con Poisson? Gracias
Tengo que resolver este problema y no se como hacerlo, me puede explicar por favor, y en excel tampoco se como se hace.
Suponga que el número de clientes que entran en un banco en una hora es una variable aleatoria de Poisson, y que la probabilidad que un cliente entre a esa hora es de 0,05. calcule lo siguiente:
1,- La probabilidad que entren 2 clientes en una hora si el número de clientes es de 20.
2,- La probabilidad que no entre ningún cliente de los 20.
3,- La probabilidad que entren 2 o menos de los 20 clientes.
4,- La esperanza matemática de los 20 clientes.
5,- La varianza de los 20 clientes.
para la solucion de este experimento de tipo poisson lo primero que se debe de recurrir ha hacer es calcular del valor esperado a encontrar el promedio de clientes que llegan al banco en una hora como se considera que por total de la muestra es 20 y la probabilidad de que un cliente entre al banco es de 0.05 entonces.
n=20
p=0.05
μ=np
μ=20*0.05=1 (Esta es la esperanza matematica o el valor esperado)
μ=1
Ahora se procede a calcular los apartados con la siguiente formula de la distribucion de poisson.
p(μ,x)=(e^(-μ)*(μ)^(x))/x!
1) p(x=2)= (e^(-1)*(1)^(2))/2!=0.1839397206
2) p(x=0)=(e^(-1)*(1)^(0))/0!=0.3678794412
3)p(x<=2)=p(x=0)+p(x=1)+p(x=2)
p(x<=2)=(e^(-1)*(1)^(0))/0!+(e^(-1)*(1)^(1))/1!+(e^(-1)*(1)^(2))/2!
p(x<=2)=0.9196986029
4) este ya se habia calculado al inicio y es
μ=1
5) Para calcular la varianza se utiliza la siguiente formula
σ^2=np(1-p)
σ^2=20*0.05*0.95=0.95
Esa es la solucion manual del ejercicio espero de que pueda serle de mucha ayuda...
Distribución de Poisson
Suponga que el número medio de clientes que llegan por minuto al banco entre el medio dia y la 1:00 P.M es igual a 3.
¿Cúal es la probabilidad de que lleguen exactamente dos clientes?
¿Cúal es la probabilidad de que lleguen más clientes?
Publicar un comentario