Un histograma es un diagrama de barras constituido por rectángulos cuyas bases corresponden a la anchura de cada clase, y las alturas a las respectivas frecuencias. Es un diagrama bastante usado cuando los datos están agrupados en clases.
El histograma es el gráfico estadístico por excelencia, cuyas ventajas son:
- Es útil para apreciar la forma de la distribución de los datos, si se escoge adecuadamente el número de clases y su amplitud.
- Se puede presentar como un gráfico definitivo en un reporte.
- Se puede utilizar para comparar dos o más muestras o poblaciones.
- Se puede refinar para crear gráficos más especializados, por ejemplo la pirámide poblacional.
- Las observaciones individuales se pierden.
- La selección del número de clases y su amplitud que adecuadamente representen la distribución puede ser complicado. Un histograma con muy pocas clases agrupa demasiadas observaciones y uno con muchas deja muy pocas en cada clase. Ninguno de los dos extremos es adecuado.
La función para diseñar histogramas en R es: hist(), y para su uso, expondremos un ejemplo didáctico de aplicación.
Por ejemplo, disponemos de los siguientes datos, que corresponde a los tiempos, en segundos, de una CPU de 25 trabajos realizados por un ordenador:
| 0.02 | 0.15 | 0.19 | 0.47 | 0.71 | 0.75 | 0.82 | 0.92 | 0.96 | 1.16 | 1.17 | 1.23 | 1.38 |
| 1.40 | 1.59 | 1.61 | 1.94 | 2.01 | 2.16 | 2.41 | 2.59 | 3.07 | 3.53 | 3.76 | 4.75 |
Para almacenarlos en R, existen varios métodos, en este caso, usamos la función scan():
> datos <- scan()
1: 0.02 0.15 0.19 0.47 0.71 0.75 0.82 0.92 0.96 1.16 1.17 1.23 1.38
14: 1.40 1.59 1.61 1.94 2.01 2.16 2.41 2.59 3.07 3.53 3.76 4.75
26:
Si usamos ahora la función hist() con los datos anteriores obtenemos:
Pero la función va más allá, ya que tal y como se muestra, sin tratamiento, no tiene mucho sentido ni valor estadístico, es por ello que este capítulo tratará de cómo usar de forma óptima dicha función para que la información gráfica que obtengamos sea de interés.
Siguiendo con los datos anteriormente dados, los vamos a tratar antes de usar la función hist(), lo primero, es saber en cuantas clases será de utilidad dividir los datos.
Por ejemplo, si queremos agrupar los datos en 7 clases y ampliando el intervalo a [0.02, 4.92] y sin saltos entre intervalo, es decir, subinterválos contínuos.
Lo primero, es obtener la longitud de cada clase será:
h = (b - a)/p = (4.92 - 0.02)/ 7 = 0.7
En la función hist() existe un argumento donde podemos definir los saltos de cada clase, dicho argumento es: breaks.
En nuestro caso, definiremos el límite inferior y superior y la longitud de cada intervalo, de la siguiente manera: breaks = seq(0.015, 4.92, by=0.7).
Aplicamos todo lo anterior a la función hist():
> hist(datos, seq(0.015, 4.92, by=0.7))
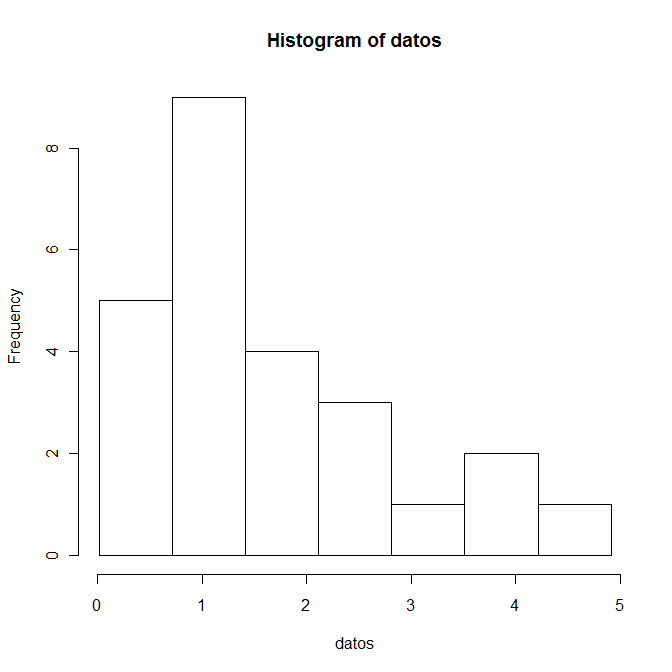
Como podemos observar, nos representa gráficamente el histograma tal y como queremos en nuestro estudio.
Pero aquí no acaba las opciones de esta función, ya que también nos puede dar información por consola, para ello, tendremos que declarar que no nos dibuje el histograma, esto se consigue con el argumento plot, es un argumento lógico, por defecto está en TRUE, quiere decir que siempre nos representa la gráfica, en cambio si lo ponemos en FALSE, no nos representará el histograma de forma gráfica pero sí nos mostrará información por consola.
Siguiendo con el ejemplo anterior obtendríamos:
> hist(datos, seq(0.015, 4.92, by=0.7), plot=F)
$breaks
[1] 0.015 0.715 1.415 2.115 2.815 3.515 4.215 4.915
$counts
[1] 5 9 4 3 1 2 1
$intensities
[1] 0.28571423 0.51428571 0.22857143 0.17142857 0.05714286 0.11428571 0.05714286
$density
[1] 0.28571423 0.51428571 0.22857143 0.17142857 0.05714286 0.11428571 0.05714286
$mids
[1] 0.365 1.065 1.765 2.465 3.165 3.865 4.565
$xname
[1] "datos"
$equidist
[1] TRUE
attr(,"class")
[1] "histogram"
Podemos observar, que nos ofrece gran cantidad de información, empezando por lo intervalos de las clases en $breaks:
| Subintervalos |
| 0.015 - 0.715 |
| 0.715 - 1.415 |
| 1.415 - 2.115 |
| 2.115 - 2.815 |
| 2.815 - 3.515 |
| 3.515 - 4.215 |
| 4.215 - 4.915 |
También nos informa de las frecuencias absolutas de cada intervalo en $counts:
Otra información que podemos obtener son las frecuencias relativas, tanto $intensities como $density nos la ofrece, ambas son lo mismo, simplemente se mantiene por compatibilidad con el lenguaje S, pero nos la da de una manera peculiar, nos ofrece la función de densidad, para obtener la frecuencia relativa debemos multiplicar estos elementos por el número de clases entre 10:
También nos ofrece las marcas de los subintervalos en $mids:
Y por último, el campo $equidist, nos informa que los intervalos tienen la misma longitud, ésto lo podemos cambiar a la hora de ejecutar la función hist().
| Subintervalos | Frecuencias absolutas, fi |
| 0.015 - 0.715 | 5 |
| 0.715 - 1.415 | 9 |
| 1.415 - 2.115 | 4 |
| 2.115 - 2.815 | 3 |
| 2.815 - 3.515 | 1 |
| 3.515 - 4.215 | 2 |
| 4.215 - 4.915 | 1 |
Otra información que podemos obtener son las frecuencias relativas, tanto $intensities como $density nos la ofrece, ambas son lo mismo, simplemente se mantiene por compatibilidad con el lenguaje S, pero nos la da de una manera peculiar, nos ofrece la función de densidad, para obtener la frecuencia relativa debemos multiplicar estos elementos por el número de clases entre 10:
| Subintervalos | Frecuencias absolutas, fi | Frecuencias relativas, hi |
| 0.015 - 0.715 | 5 | 0.28571423· (7/10) ≈ 0.2 |
| 0.715 - 1.415 | 9 | 0.51428571· (7/10) ≈ 0.36 |
| 1.415 - 2.115 | 4 | 0.22857143· (7/10) ≈ 0.16 |
| 2.115 - 2.815 | 3 | 0.17142857· (7/10) ≈ 0.12 |
| 2.815 - 3.515 | 1 | 0.05714286· (7/10) ≈ 0.04 |
| 3.515 - 4.215 | 2 | 0.11428571· (7/10) ≈ 0.08 |
| 4.215 - 4.915 | 1 | 0.05714286 · (7/10) ≈ 0.04 |
| Subintervalos | Frecuencias absolutas, fi | Frecuencias relativas, hi | Marcas |
| 0.015 - 0.715 | 5 | 0.2 | 0.365 |
| 0.715 - 1.415 | 9 | 0.36 | 1.065 |
| 1.415 - 2.115 | 4 | 0.16 | 1.765 |
| 2.115 - 2.815 | 3 | 0.12 | 2.465 |
| 2.815 - 3.515 | 1 | 0.04 | 3.165 |
| 3.515 - 4.215 | 2 | 0.08 | 3.865 |
| 4.215 - 4.915 | 1 | 0.04 | 4.565 |
Y por último, el campo $equidist, nos informa que los intervalos tienen la misma longitud, ésto lo podemos cambiar a la hora de ejecutar la función hist().
La utilidad que tiene que no se represente el histograma es poder guardar en una variable toda la información del análisis que queremos estudiar, por ejemplo, vamos a guardar en la variable x, toda la información anteriormente presentada:
> x <- hist(datos, seq(0.015, 4.92, by=0.7), plot=F)
Ahora mismo, en la variable x está toda la información que se ha presentado con anterioridad, y esto es bastante útil e interesante ya que podemos acceder a cualquier campo independientemente, por ejemplo, acceder al campo de las marcas o puntos medios:
> x$mids
[1] 0.365 1.065 1.765 2.465 3.165 3.865 4.565
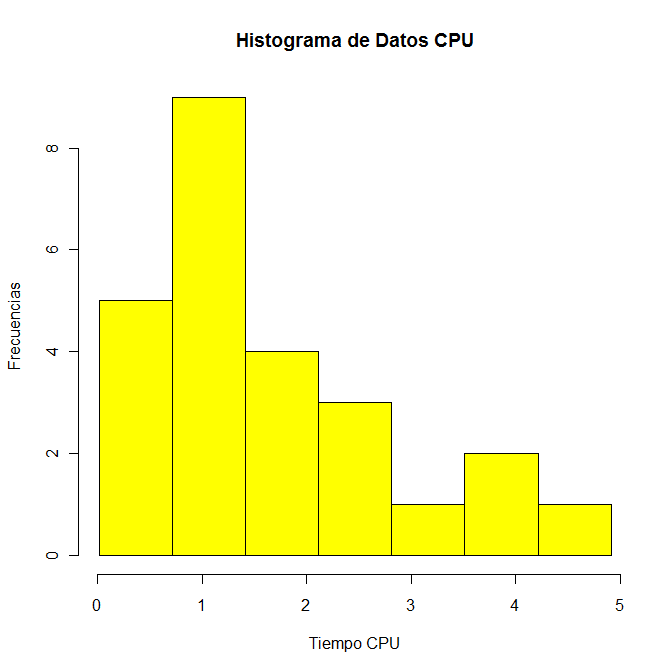
Y para concluir, la gráfica que se obtiene es totalmente personalizable, por ejemplo, para ponerle un título principal usamos el argumento main de la función hist(): Histograma de Datos CPU:
> hist(datos, seq(0.015, 4.92, by=0.7), main="Histograma de Datos CPU")
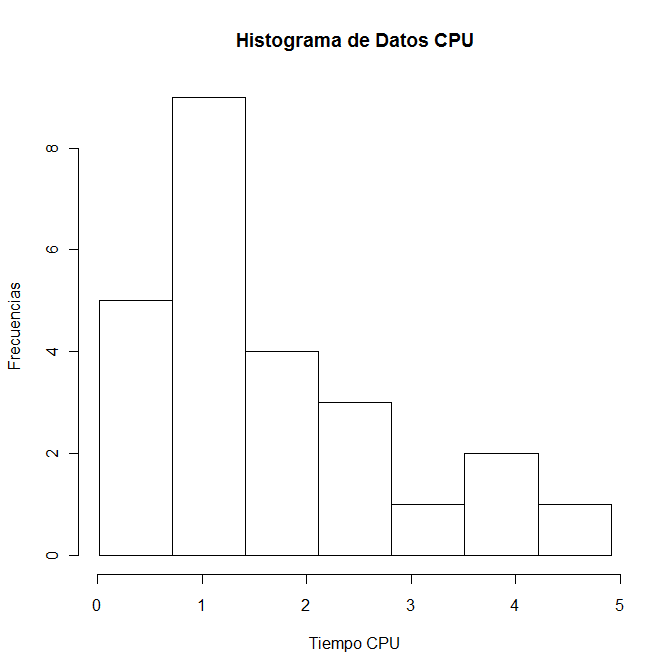
También podemos poner nombres a los ejes, para ello, usamos los argumentos xlab e ylab para el eje X e Y respectivamente
> hist(datos, seq(0.015, 4.92, by=0.7), main="Histograma de Datos CPU", xlab="Tiempo CPU", ylab="Frecuencias")
> x <- hist(datos, seq(0.015, 4.92, by=0.7), plot=F)
Ahora mismo, en la variable x está toda la información que se ha presentado con anterioridad, y esto es bastante útil e interesante ya que podemos acceder a cualquier campo independientemente, por ejemplo, acceder al campo de las marcas o puntos medios:
> x$mids
[1] 0.365 1.065 1.765 2.465 3.165 3.865 4.565
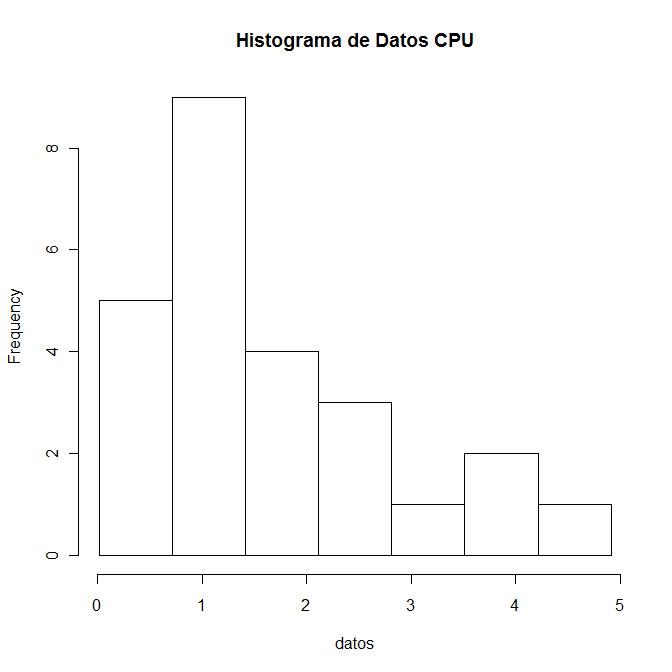
Y para concluir, la gráfica que se obtiene es totalmente personalizable, por ejemplo, para ponerle un título principal usamos el argumento main de la función hist(): Histograma de Datos CPU:
> hist(datos, seq(0.015, 4.92, by=0.7), main="Histograma de Datos CPU")
También podemos poner nombres a los ejes, para ello, usamos los argumentos xlab e ylab para el eje X e Y respectivamente
> hist(datos, seq(0.015, 4.92, by=0.7), main="Histograma de Datos CPU", xlab="Tiempo CPU", ylab="Frecuencias")
Y también podemos cambiar de color de las barras con el argumento col, para ello, disponemos de los siguientes colores:
> hist(datos, seq(0.015, 4.92, by=0.7), main="Histograma de Datos CPU", xlab="Tiempo CPU", ylab="Frecuencias", col=15)
También se puede cambiar el color del borde de los bloques, cambiar las escalas de los ejes, poder poner etiquetas, etc, para todo esto y más información, se recomienda que se use la ayuda:
> ?"hist"
Para concluir, el histograma es un gráfico bastante usado y en R disponemos las herramientas necesarias para su diseño, estudio y creación de forma fácil y factible.
- Código: 0 o 8: Tonalidad blanca.
- Código: 1 o 9: Tonalidad negro.
- Código: 2 o 10: Tonalidad rojo.
- Código: 3 o 11: Tonalidad verde.
- Código: 4 o 12: Tonalidad azul.
- Código: 5 o 13: Tonalidad magenta.
- Código: 6 o 14: Tonalidad violeta.
- Código: 7 o 15: Tonalidad amarillo.
> hist(datos, seq(0.015, 4.92, by=0.7), main="Histograma de Datos CPU", xlab="Tiempo CPU", ylab="Frecuencias", col=15)
También se puede cambiar el color del borde de los bloques, cambiar las escalas de los ejes, poder poner etiquetas, etc, para todo esto y más información, se recomienda que se use la ayuda:
> ?"hist"
Para concluir, el histograma es un gráfico bastante usado y en R disponemos las herramientas necesarias para su diseño, estudio y creación de forma fácil y factible.





13 comentarios:
Hola, me da mucho gusto saber que hay gente interesada en realizar este tipo de trabajos, la información es muy buena y desde luego de gran ayuda.
Buenas:
Me alegra que te sea de utilidad y agrado.
Un saludo.
Hola,
primero que nada felicidades por tu página. Ahora quisiera preguntarte la siguiente duda:
Se quiere sacar un histograma relacionando el número de familias por su número de hijos:
--------------------
| Hijos | Familias |
--------------------
| 0 | 4 |
| 1 | 8 |
| 2 | 2 |
| 3 | 10 |
| 4 | 11 |
--------------------
El problema es que estoy aprendiendo a usar R y aún tengo problemas para resolverlos. Gracias de antemano.
Buenas Félix:
Si sigues los pasos de este capítulo y entiendes el concepto de histograma, no te será difícil crear el que me pides.
Te lo pongo por pasos:
1. Declarar la variable de datos:
NumHijos<-c(0,0,0,0,1,1,1,1,1,1,1,1,2,2,3,3,3,3,3,3,3,3,3,3,4,4,4,4,4,4,4,4,4,4,4)
2. Tener en cuenta que el dato inferior es 0 y el superior es 4, estos datos nos dará la longitud de la clase, sabiendo que el paso es de 5 (el número de saltos que has especificado en tu problema). Por lo tanto, la longitud, si haces los cálculos, es de 0.8.
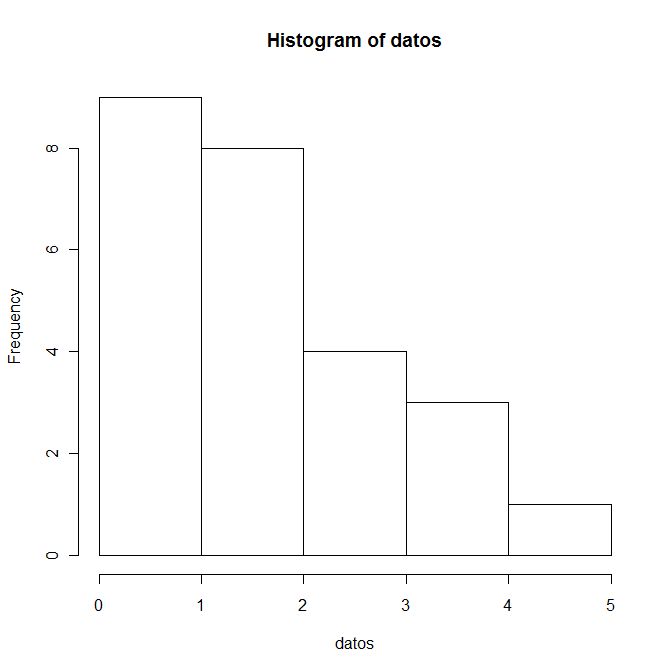
Ahora bien, si lo ponemos directamente tal cual, tendremos la representación de forma correcta pero en el Eje X (Número de Hijos), nos saldrá de forma extraña. Compruébalo con la siguiente instrucción:
hist(NumHijos,breaks=seq(0,4,by=0.8))
Para arreglar el Eje X, nos olvidaremos de definir la longitud de los intervalos, simplemente, impondremos que lea los datos desde un poco menor al dato más pequeño y un poco mayor al dato más grande.
Por lo tanto, la solución a tu problema, es tal y cómo te muestro en la siguiente instrucción:
hist(NumHijos,breaks=c(-0.5:4.5),ylim=c(0,12))
Gracias por tu comentario y espero haberte ayudado.
hola me es de mucha utilidad lo que compartes muchas gracias queria saber si me podrias orientar con este problema: A finales de octubre intenté hacer pan de muerto para el altar de todos santos de mi casa. Después de mesclar todos los ingredientes y hacer todo el ritual de amasado, dejé levar el producto de este trabajo durante de 2 horas y media (tiempo necesario para obtener el crecimiento de la masa), pero encontré que la masa seguía igual, es decir no produjo las burbujas propias del levado correcto. Después de disertar con mi esposa e hijos sobre las posibles causas de esta catástrofe, llegamos a la conclusión que la culpable fue la levadura, que ya estaba “inactiva” y por tanto no produjo el efecto deseado: el levado de la masa. Dime con lujo de detalle qué debo hacer para poner a prueba esta hipótesis, si considero que la levadura tiene una fecha de caducidad específica que corresponde a septiembre de 2011. Dime qué enfoque de trabajo debo emplear para responder esta interrogante
Buenas:
Tal cual lo planteas, no hay manera de realizar datos estadísticos, respecto a realizar una prueba de hipótesis, los pasos a seguir serían los siguientes:
1. Evaluar si el estudio sigue una distribución normal (para adaptarlo a un estudio paramétrico).
2. En caso afirmativo: Realizar la prueba de hipótesis de que la activación media de la levadura es de 2h30 (hipótesis nula) o no (hipótesis alternativa).
Como podrás ver, es necesario datos adicionales para realizar el estudio como por ejemplo, medias de activación de la levadura empleada (algunas serán de 2h30, 2h00, 3h00 etc).
También podrías realizar un estudio de probabilidad, pero para ello, necesitarías las probabilidades de activación de la levadura, la de no activación etc.
En fin, un estudio o trabajo de estadística es necesario, siempre, unos datos con los cuales podamos trabajar para llegar a dar una conclusión viable.
Un saludo y gracias por tu comentario.
hola me gustaría saber sobre seq(0.015, 4.92, by=0.7))
de donde sacaste el 0.015 entiendo lo demas pero por que le pusiste ese valor te lo agradecere mucho
Buenas:
Cuando se define los intervalos, siempre tienes que poner un poco por debajo y un poco por arriba, para que R pueda recoger y procesar los datos correctamente.
El 0.015 corresponde a un poco por debajo del 0.2.
Un saludo y gracias por tu comentario.
Hola,
Quisiera saber cómo se modifica la escala del eje y, de decimal a notación científica.
Gracias!
Buenas:
Para ello, deberás emplear la opción breaks que encontrarás en la ayuda de la función.
Un saludo.
Gracias estuvo buena la guía muy clara felicitaciones!!!!, me ayudo.
Excelente!! me ayudó muchisimo. Muchas gracias Manuel Caballero
buenos dias.
Muy buena entrada, me despeja muchas dudas, excepto una, tengo una tabla con 12000 registros, la importe con read.dbf, pero necesito hacer un histograma de frecuencia de una de sus columnas, es posible que R lea directamente la columna como la variable de datos, sin declararla "a mano" como resolviste el caso de Manuel Caballero???
yo estudio tambien SQL, y es posible relacionando la columna a la tabla como el objeto a analisar ejemplo:
SUM("tabla.columna");
estoy buscando documentacion y no encuentro nada relacionado a mi problema....
agradesco de antemano la colaboracion.
Publicar un comentario