Problema 2: Normal Tipificada

Ej2. En cada caso, determine el valor de la constante c que hace correcto el enunciado de probabilidad:

a) Φ(c) = 0.9838.

b) P(0 ≤ Z ≤ c) = 0.291.

c) P(Z > c) = 0.121.

d) P(-c ≤ Z ≤ c) = 0.668.



Apartado a)

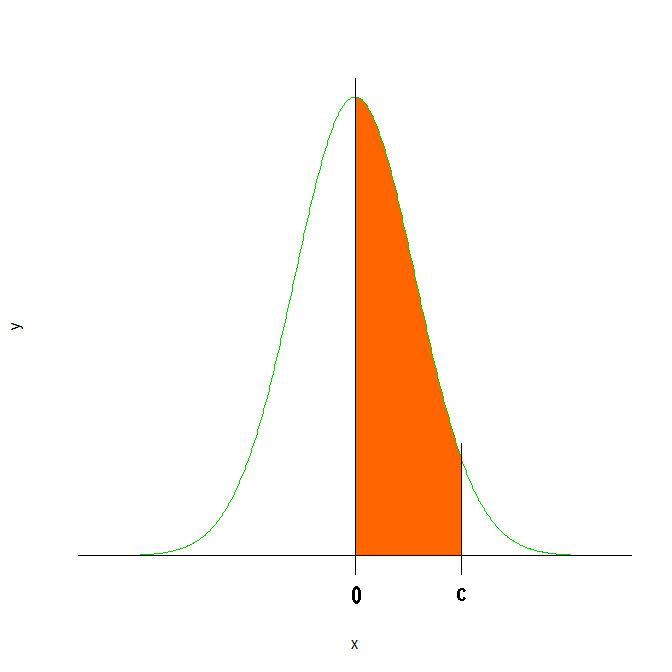
Primero nos hacemos una idea gráficamente de lo que nos ofrece el enunciado:

Teniendo en cuenta que la tabla que proporciona este blog sólo muestra el área de media curva (por ser simétrica), por lo tanto:

0.5 + Φ(c) = 0.9838

Despejamos:

Φ(c) = 0.9838 - 0.5 = 0.4838

Entonces, debemos hallar en la tabla dicho valor:

Por lo tanto, la solución a este apartado es: c = 2.14.


Apartado b)

Al igual que en el apartado anterior, nos hacemos una idea gráficamente de lo que nos ofrece el enunciado:

Teniendo en cuenta que la tabla que proporciona este blog sólo muestra el área de media curva (por ser simétrica), por lo tanto:

P(0 ≤ Z ≤ c) = P(Z = c) - P(Z = 0) = [0.5 + Φ(c)] - [0.5 + Φ(0)] = Φ(c)

Despejamos:

Φ(c) = 0.291

Debemos hallar en la tabla dicho valor:

Por lo tanto, la solución a este apartado es: c = 0.81.

Apartado c)

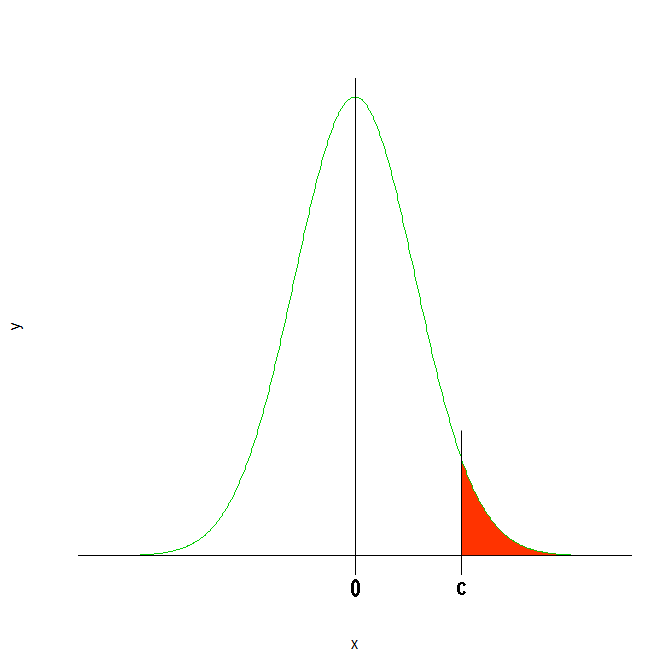
Actuamos como en los apartados anteriores, nos hacemos una idea gráficamente de lo que nos ofrece el enunciado:

Teniendo en cuenta que la tabla que proporciona este blog sólo muestra el área de media curva (por ser simétrica), y usamos la regla del complemento:

P(Z > c) = 1 - P(Z ≤ c) = 1 - [0.5 + Φ(c)] = 0.121

Despejamos:

Φ(c) = 0.379

Entonces, debemos hallar en la tabla dicho valor:

Por lo tanto, la solución a este apartado es: c = 1.17.

Apartado d)

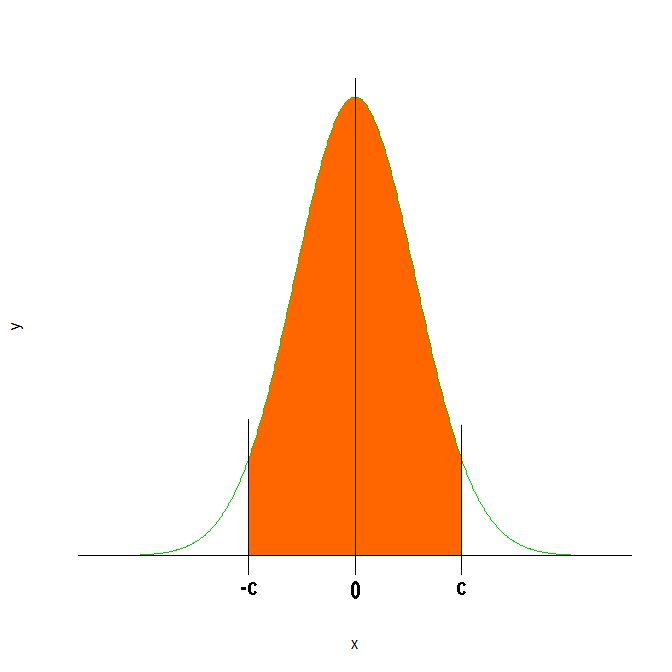
Primero nos hacemos una idea gráficamente de lo que tenemos que nos ofrece el enunciado:

Teniendo en cuenta que la tabla que proporciona este blog sólo muestra el área de media curva (por ser simétrica), y usamos la regla del complemento:

P(-c ≤ Z ≤ c) = 0.668 = [0.5 + Φ(c)] - [1 - (0.5 + Φ(c))] = 2Φ(c)

Despejamos:

Φ(c) = 0.668/2 = 0.334

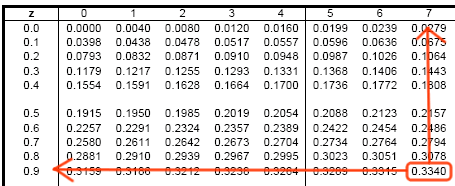
Entonces, debemos hallar en la tabla dicho valor:

Por lo tanto, la solución a este apartado es: c = 0.97.