Problema 1: Normal Tipificada

Ej1. Calcule las siguientes probabilidades normales tipificadas:

a) P(Z ≤ 1.25).

b) P(Z > 1.25).

c) P(Z ≤ -1.25).

d) P(-0.38 ≤ Z ≤ 1.25).


Apartado a)

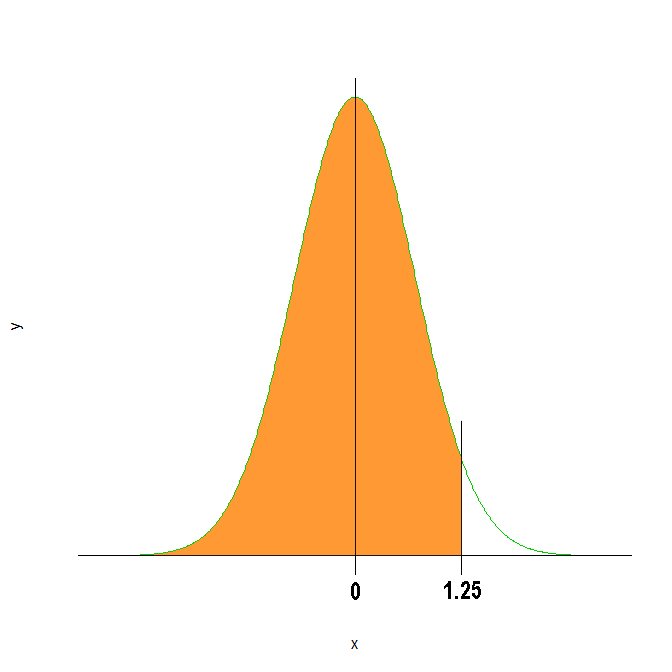
Primero nos hacemos una idea gráficamente de lo que tenemos que calcular:

Teniendo en cuenta que la tabla que proporciona este blog sólo muestra el área de media curva (por ser simétrica), debemos añadirle el 0.5 restante, por lo tanto:

P(Z ≤ 1.25) = 0.5 + Φ(1.25)

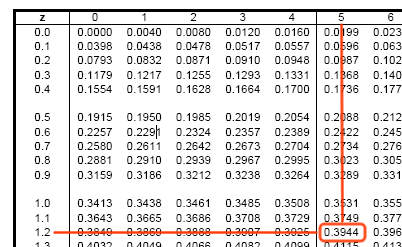
Entonces, debemos hallar en la tabla dicho valor, tendremos que buscar el 1.2 en la primera columna de la tabla y el decimal 5 en la primera fila de la tabla:

Por lo tanto, la solución a este apartado es:

P(Z ≤ 1.25) = 0.5 + Φ(1.25) = 0.5 + 0.3944 = 0.8944

Apartado b)

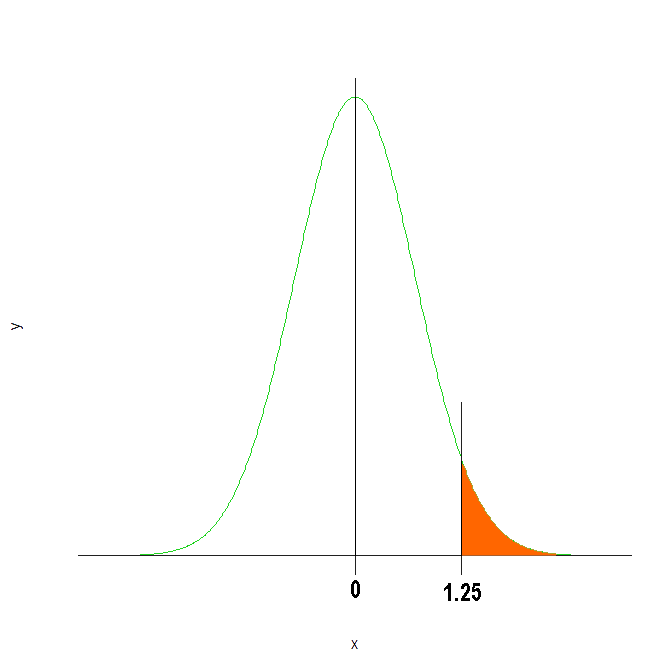
Procedemos igual que en apartado anterior, haciéndonos una idea gráficamente de lo que tenemos que calcular:

Para el cálculo de esta probabilidad, usamos la regla del complementario:

P(Z > 1.25) = 1 - P(Z ≤ 1.25)

Teniendo en cuenta que la tabla que proporciona este blog sólo muestra el área de media curva (por ser simétrica), debemos añadirle el 0.5 restante, por lo tanto:

P(Z ≤ 1.25) = 0.5 + Φ(1.25)

Obtenemos el valor como se ilustra en el Apartado a). Por lo tanto, la solución a este apartado es:

P(Z > 1.25) = 1 - P(Z ≤ 1.25) = 1 - [0.5 + Φ(1.25)] = 1 - 0.8944 = 0.1056

Apartado c)

Operamos:

P(Z ≤ -1.25) = P(Z > 1.25) = 1 - P(Z ≤ 1.25)

Por lo que nos queda el mismo problema que nos pedía el Apartado b), por lo tanto, la solución es: 0.1056.

Esto es así porque la curva de Gauss es simétrica.

Apartado d)

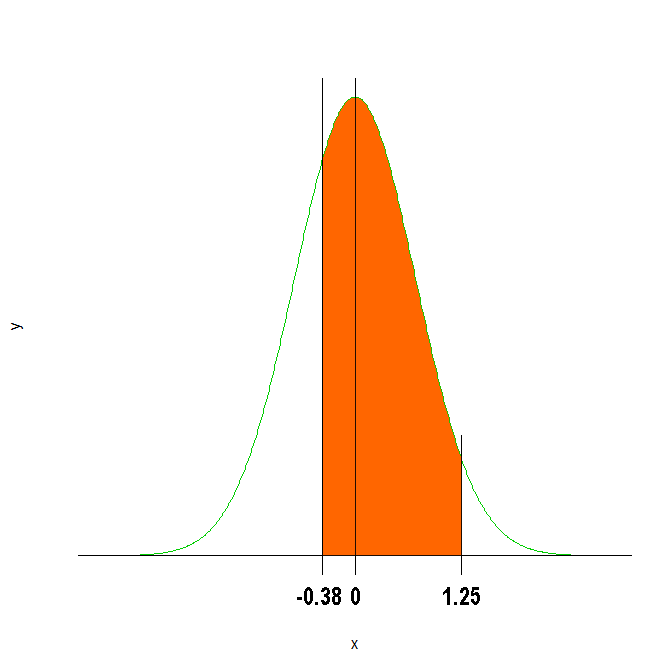
Procedemos igual que en los apartados anteriores, haciéndonos una idea gráficamente de lo que tenemos que calcular:

Calculamos la probabilidad:

P(-0.38 ≤ Z ≤ 1.25) = P(Z = 1.25) - P(Z = -0.38)

Tenemos que tener en cuenta que las tablas que disponemos no contempla datos en la parte negativa del eje de abscisa X de la curva por lo que tendremos que usar su complementario al igual que, sólo disponemos, por tablas, los valores de la mitad del área de la curva.

Por lo tanto:

P(-0.38 ≤ Z ≤ 1.25) = (0.5 + Φ(1.25)) - [1 - (0.5 + Φ(0.38))]

El valor de 1.25 lo conocemos de los apartados anteriores: 0.3944, obtenemos el de 0.38 por tablas:

Por lo tanto, la solución de este apartado es:

P(-0.38 ≤ Z ≤ 1.25) = (0.5 + 0.3944) - [1 - (0.5 + 0.1480)] = 0.5424