Problema9: Cartas de Control

Ej9. La característica de calidad X de un artículo tiene distribución normal. Los límites de control 3-sigma de una carta X con muestras de tamaño 5 son:

· LSC = 131.41.
· LIC = 106.59.

Determinar:

a) Las estimaciones de la media y de la varianza del proceso.

b) Los límites de especificación son 120±20. Estime los cocientes de capacidad CCP y CCPk. ¿Cuál de ellos describe mejor la habilidad del proceso para producir artículos que cumplan las especificaciones?¿Por qué?

c) Calcule el porcentaje de artículos que cumplen las especificaciones. ¿Qué medidas correctoras propondría para elevar este porcentaje?


Realizamos una recopilación de datos ofrecidos por el enunciado del problema:

· Carta de control de medias X, sigue una distribución normal: X~N(μ, σ).
· Límite de control superior: LSC = 131.41.
· Límite de control inferior: LIC = 106.59.
· Tamaño de la muestra: n = 5.

Pasamos a resolver los distintos apartados del problema.


Apartado a)

Para obtener la media, es decir, el límite central del proceso de control, realizamos la media de los límites de control superior e inferior:

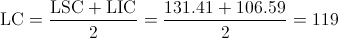
Por lo tanto, la estimación de la media del proceso, el límite central, es 119.

Debemos obtener la varianza, sabemos que la expresión para obtener un estimador de la desviación estándar es:

·

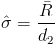
Pero no sabemos cual es el valor del rango, así que empleamos los límites de control superior e inferior de control, para obtener el valor del rango:

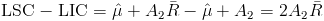
Despejamos el parámetro del rango:

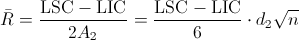
Ya disponemos del valor del rango, ahora, sustituimos en la expresión del estimador de la desviación estándar:

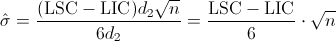
Sustituimos valores:

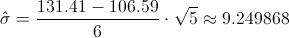
Por lo tanto, la varianza es: 9.249868² ≈ 85.560058.


Apartado b)

En este apartado nos dan los límites de especificaciones:

· Límite de especificación superior: LES = 120+20 = 140.
· Límite de especificación inferior: LEI = 120-20 = 100.

Empleamos las expresiones para obtener los parámetros pedidos por este apartado.

· Capacidad Potencial del Proceso:

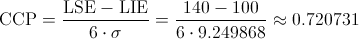
· Coeficiente de Capacidad Real del Proceso:

Por lo tanto: CCP_k = 0.684694.

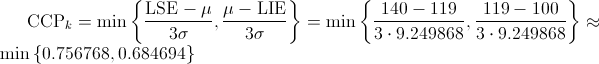
El coeficiente segundo, CCP_k, describe mejor la habilidad del proceso para producir artículos que cumplan las especificaciones ya que tiene en cuenta el ligero descentrado existente.


Apartado c)

En este apartado nos piden obtener la probabilidad de artículos que cumpan con las especificaciones, por lo tanto, lo que debemos hallar es:

P(100 ≤ X ≤ 140)

Ya que el proceso de control de muestras, X, sigue una distribución normal, tipifico:

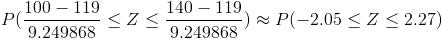
Por lo tanto, tenemos:

P(100 ≤ X ≤ 140) = (0.5 + Φ(2.27)) - [1 - (0.5 + Φ(2.05))] = Φ(2.27) + Φ(2.05)

Buscamos en la tabla de la Normal y otenemos la probabilidad deseada:

P(100 ≤ X ≤ 140) = Φ(2.27) + Φ(2.05) = 0.4884 + 0.4798 = 0.9682

El porcentaje de artículos que cumplen las especificaciones es: 96.82%.

Para aumentar este porcentaje, pueden tomarse dos medidas:

· Centrar el proceso.
· Reducir la variabilidad, es decir, el valor de σ.

Lo que es muy importante es que nunca se deben modificar las especificaciones, ya que son exigencias impuestas por el fabricante, para que los artículos sean como tiene que ser, es decir, que si se modificaran ya no serían los artículos deseados, sino otros.