R: Coordenadas Polares

Aunque ya sabemos que el lenguaje R está destinado, principalmente, a todo lo que tenga que ver con la estadística, también podemos emplearlo para otros menesteres gracias a las funciones y scripts que podemos diseñar nosotros mismos.

Y eso es precisamente, la base de este capítulo, concretamente en dotar a R de poder representar gráficamente curvas en Coordenadas Polares.

Lo que se pretende es diseñar una función que devuelva, de forma gráfica, la representación de una curva en el Sistema Polar.

¿Y por qué diseñar una función de estas características? Pues simple y llanamente es, porque a la versión de escribir este capítulo 2.9.2, no se puede representar en dicho sistema.

No nos adentraremos en qué consiste el Sistema Polar y en la forma de obtenerlo mediante Coordenadas Cartesianas, lo doy por sabido, simplemente hacer una mención especial, en forma de homenaje, a René Descartes, que gracias a él, supuso un gran avance la representación y diagramas en Coordenadas Cartesianas en el ámbito de las matemáticas.

Dicho esto, centrémonos en la esencia de este capítulo, el diseño de una función que devuelve gráficamente una curva en el Sistema Polar.

El nombre de la función será: polar, la cual tendrá tres parámetros de entrada llamados: theta, r y color, y devolverá de forma gráfica, la curva dada en el sistema polar.

El papel que desempeñan los parámetros de entrada de la función polar es:

• theta: Dimensión de representación de nuestra curva.

• r: La curva a representar.

• color: Definimos el color que tomará la curva a representar. Se rige por los valores nominales del propio lenguaje R, por defecto, el color azul es el elegido.
  

La función en sí, es la siguiente:

#######################################################################
#
# Este archivo es propiedad intelectual del blog Aqueronte,
# cuya dirección web, es la siguiente:
#                                                      
#                   http://unbarquero.blogspot.com/       
#
# Se permite cualquier modificación del archivo siempre y cuando
# se mantenga la autoría del autor.
#
# El autor no se responsabiliza de las consecuencias que pueda
# ocasionar éste código debido a un uso inadecuado del mismo.
#
#######################################################################
#
# Función: Polar                  Versión:   vs0.0
# Fecha:   22/09/09               R Versión: 2.9.2
#
# Autor:    Manuel Caballero
# Compañía: Hades
#
#######################################################################
#
# Notas: Esta función dibuja en coordenadas polares.
#
# Datos de Entrada:
#          · theta: Dimensión de la curva a representar.
#          · r:     Curva a representar.
#          · color: Color de la curva a representar, por defecto azul.
#
#######################################################################
polar <- function (theta, r, color=4){
  y <- 0
  x <- 0
  ejex <- 1

  for (i in 1:length(r)){
    if(is.nan(r[i])== T){
      r[i] <- 0
    }
  }

  angulo <- seq(-max(theta),max(theta),by=theta[2]-theta[1])
  y <- r*sin(theta)
  x <- r*cos(theta)
  plot.new()
  plot.window(xlim = c(-max(r), max(r)), ylim = c(-max(r), max(r)), asp = 1)

  aux <- max(r)
  # Dibuja los ejes.
  while (aux > 0){
    fi <- aux*sin(angulo)
    cir <- aux*cos(angulo)
    points(cir,fi,pch="-",col="gray",cex=0.3)
    text(ejex+0.2,-0.2,ejex,col="gray")
    ejex <- ejex + 1
    aux <- aux - 1
  }

  abline(v=((max(cir)+min(cir))/2),col="gray")
  abline(h=((max(cir)+min(cir))/2),col="gray")
  segments(-max(r)+0.5,-max(r)+0.5,max(r)-0.5,max(r)-0.5,col="gray")
  segments(-max(r)+0.5,max(r)-0.5,max(r)-0.5,-max(r)+0.5,col="gray")

  points(x,y,pch=20,col=color,cex=1)
}

Para corroborar que la función polar funciona de forma correcta, vamos a representar varias curvas características en forma polar.

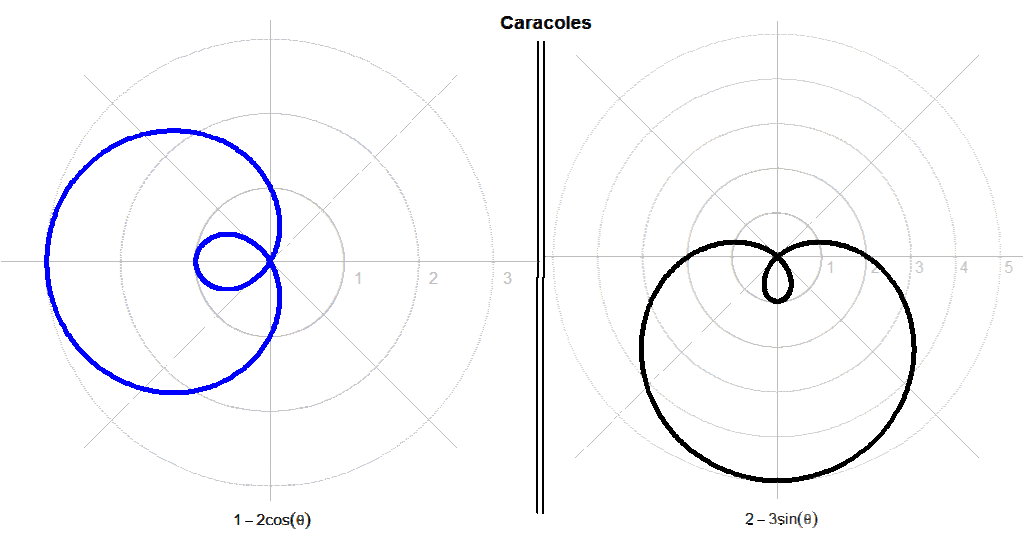
Caracoles.

Este tipo de curvas presentan la siguiente expresión:

• r = b ± a·cos(θ)

• r = b ± a·sen(θ)

Vamos a representar este tipo de curvas, para ello, definimos previamente la dimensión y declaramos la curva.

Para este ejemplo, representaremos ambos tipos de curva entre [-π, π].

> dim <- seq(-pi, pi, by=pi/300)

Teniendo en cuenta la relación de los parámetros a y b, obtenemos distintas gráficas.

- Si: (b/a) < .1:

Declaramos las curvas con restricción expuesta:

> r <- 1-2*cos(dim)
> s <- 2-3*sin(dim)

Cuya representación en el sistema polar es:

> polar(dim,r,"blue")
> polar(dim,s,"black")

- Si: 1 < .(b/a) < .2:

Declaramos las curvas con restricción expuesta:

> r <- 3-2*cos(dim)
> s <- 4-3*sin(dim)

Cuya representación en el sistema polar es:

> polar(dim,r,"green")
> polar(dim,s)

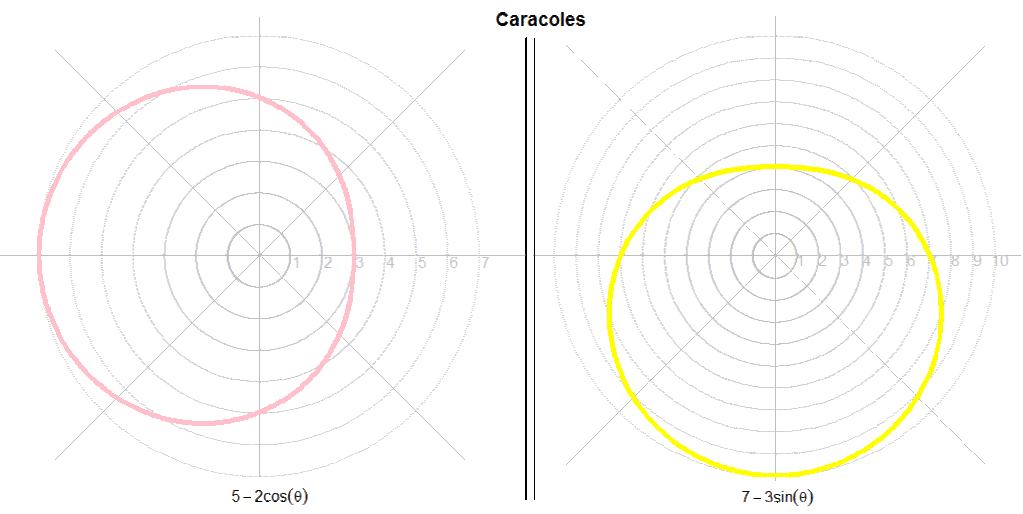
- Si: (b/a) > 2:

Declaramos las curvas con restricción expuesta:

> r <- 5-2*cos(dim)
> s <- 7-3*sin(dim)

Cuya representación en el sistema polar es:

> polar(dim,r,"pink")
> polar(dim,s,"yellow")

Cardioides.

Este tipo de curvas es un caso particular de las Caracoles cuando los parámetros son: a = b, presentan la siguiente expresión:

• r = a·[1 ± cos(θ)]

• r = a·[1 ± sen(θ)]

Vamos a representar este tipo de curvas, para ello, definimos previamente la dimensión y declaramos la curva.

Para este ejemplo, representaremos ambos tipos de curva entre [-π, π].

> dim <- seq(-pi, pi, by=pi/300)

Declaramos las curvas:

> r <- 1-1*cos(dim)
> s <- 1-1*sin(dim)

Cuya representación en el sistema polar es:

> polar(dim,r)
> polar(dim,s,"red")

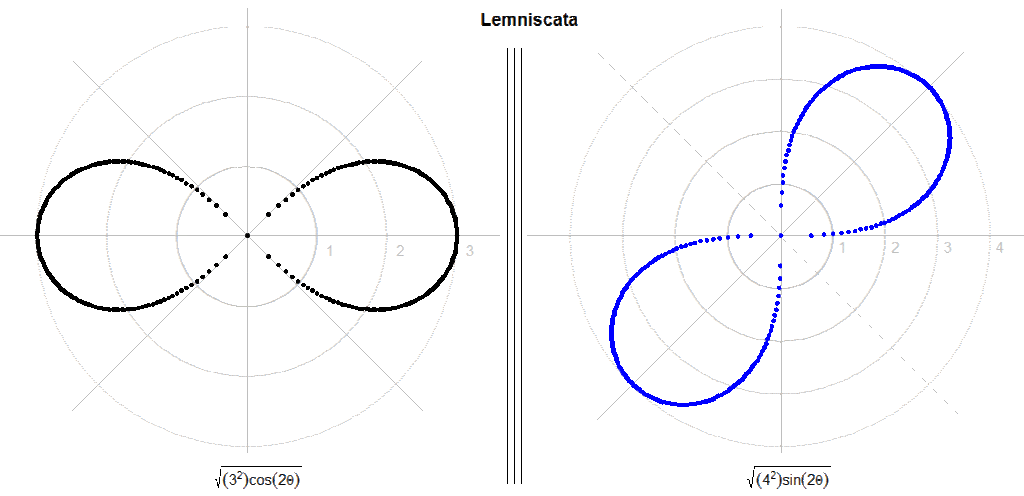
Lemniscatas.

Este tipo de curvas presentan la siguiente expresión:

• r² = a²·cos(2θ)

• r² = a²·sen(2θ)

Vamos a representar este tipo de curvas, para ello, definimos previamente la dimensión y declaramos la curva.

Para este ejemplo, representaremos ambos tipos de curva entre [-π, π].

> dim <- seq(-pi, pi, by=pi/300)

Declaramos las curvas:

> r <- sqrt((3^2)*cos(2*dim))
> s <- sqrt((4^2)*sin(2*dim))

En ambos casos, R protestará dando el siguiente mensaje:

Warning message:
In sqrt((3^2) * cos(dim)) : Se han producido NaNs

Con dicho mensaje, nos indica que para ciertos valore de la dimensión especificada, no existen valores reales y se sustituyen por NaN.

Los NaN no nos debe preocupar ya que la función polar() está capacitada para tratar con estos valores peculiares.

Cuya representación en el sistema polar es:

> polar(dim,r,"black")
> polar(dim,s)

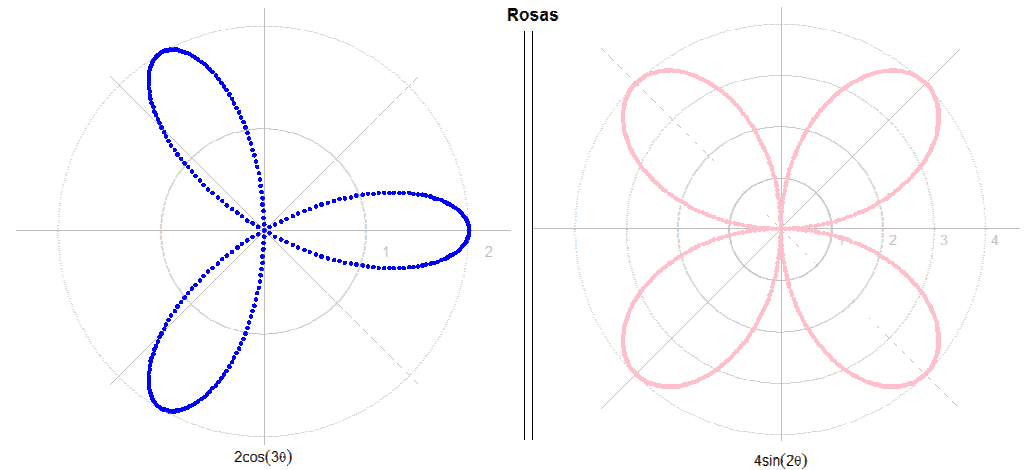
Rosas.

Este tipo de curvas presentan la siguiente expresión:

• r = a·cos(nθ)

• r = a·sen(nθ)

Si n es impar, la rosa tiene n-pétalos mientras que, si n es par, la rosa tiene 2n-pétalos.

Vamos a representar este tipo de curvas, para ello, definimos previamente la dimensión y declaramos la curva.

Para este ejemplo, representaremos ambos tipos de curva entre [-π, π].

> dim <- seq(-pi, pi, by=pi/300)

Declaramos las curvas:

> r <- 2*cos(3*dim)
> s <- 4*sin(2*dim)

Cuya representación en el sistema polar es:

> polar(dim,r)
> polar(dim,s, "pink")

---

Se puede descargar el script Polar.r del siguiente enlace:

		Polar.r
		Polar.r

---

Para concluir, esta función habilita al lenguaje R a realizar gráficas en el Sistema Polar, pero hay que tener en cuenta que tardará mas o menos tiempo en conseguir la gráfica dependiendo de la dimensión que definamos. A mayor dimensión, mayor tiempo de espera en ejecutarse.

Aunque los tiempos de ejecución no son altos en general, por ejemplo, representemos la espiral de Fermat, en el intervalo [-20π, 20π]:

> dim <- seq(-20*pi, 20*pi, by=pi/300)

Cuya expresión matemática es:

> r <- dim^(1/2)

Vamos a evaluar el tiempo que tarda en ejecutarse:

> system.time(polar(dim,r))
...user...system...elapsed
...1.31.....4.26.........5.63

Vemos que tarda en representar la curva en el intervalo definido un tiempo total de 5.63 segundos. Por cierto, la curva representada es:

Realmente no es mucho el tiempo de ejecución, ya que debe representar 12001 puntos, lo comprobamos:

> length(dim)
[1] 12001

El mayor tiempo que requiere la función polar() es en la representación de los ejes, pero hay que estar tranquilo, ya que para dimensiones normales, el tiempo de espera es casi nulo.

Y bueno, he aquí el final de este capítulo, donde se muestra como dotar de herramientas que no vienen incorporadas en R por defecto, como el presente caso, las Coordenadas Polares.