Problema16: Análisis de Regresión

Ej16. Se pretende calibrar un cromatógrafo, instrumento usado para detectar cantidades muy pequeñas de sustancias. Para ello, se preparan cuatro probetas con distintas cantidades de una sustancia dada y para cada una de ellas se realizan cuatro medidas con el aparato:

Cantidad	Medida		Cantidad	Medida
0.25	6.55		5	211
0.25	7.98		5	204
0.25	6.54		5	212
0.25	6.37		5	213
1	29.7		20	929
1	30.0		20	905
1	30.1		20	922
1	29.5		20	928

Determinar:

a) Ajuste los datos de la tabla a un modelo lineal.

b) Calcule un intervalo de confianza al 95% para la pendiente de la recta de regresión. ¿Es significativa la regresión lineal a un nivel de significación 0.05?.

c) Calcule el coeficiente de determinación e interprete el resultado.


Antes de empezar a resolver los apartados propuestos, hacemos una recopilación de datos que podemos extraer de la tabla dada, ya que posteriormente serán de gran utilidad.

· n = 16

·

·

·

·

·

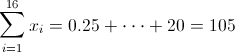
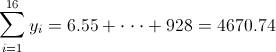
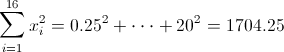
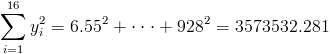
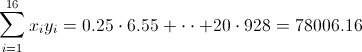
Pasamos a resolver los distintos apartados que nos ofrece el enunciado del problema.


Apartado a)

Para calcular la pendiente, la expresión matemática es:

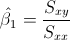
Para obtener su valor, necesitamos saber los valores de Sxy y Sxx:

·

·

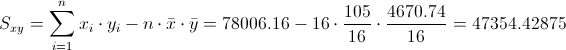
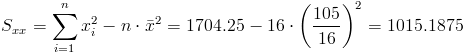
Por lo tanto, la pendiente es:

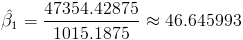
Una vez obtenida la pendiente, podemos tener el valor del estimador para la ordenada:

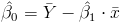
Sustituimos valores:

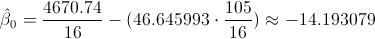
Por lo tanto, la ecuación de regresión ajustada es:

y(x) = -14.193079 + 46.645993·x

Siendo:

· y ≡ Medida.
· x ≡ Cantidad.

Apartado b)

En este apartado nos piden obtener un intervalo de confianza para la pendiente de la recta de regresión, cuya expresión matemática es:

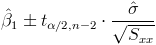
Al 95%, obtenemos α:

100(1 - α) = 95

Despejamos el parámetro que nos interesa: α = 0.05, tenemos, en la tabla t-Student:

· t_{α/2, n -2} = t_{0.05/2, 16 -2} = t_{0.025, 14} = 2.1448

Debemos obtener el valor del estimador de la desviación estándar:

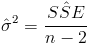
Siendo:

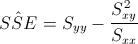
Debemos obtener Syy:

·

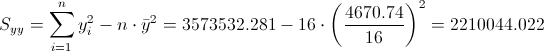
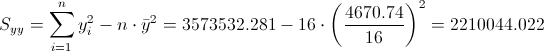
Ya tenemos todos los datos necesarios para estimar la varianza:

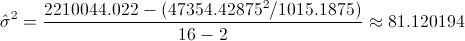
Sustituimos valores en la expresión del intervalo de confianza para la pendiente:

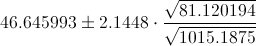
Por lo tanto, el interválo para la pendiente de la recta de regresión, al 95% es, aproximadamente:

[46.039706, 47.252280]

Al no contener el valor cero el intervalo de confianza, podemos afirmar que es significativa la regresión lineal para el propuesto nivel de significación.


Apartado c)

Para obtener el coeficiente de determinación, empleamos su expresión matemática:

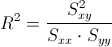
Disponemos de todos los datos necesarios para determinarlo ya que han sido calculados en apartados anteriores.

Sustituimos valores y obtenemos el resultado del coeficiente de determinación:

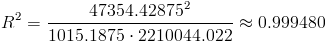
Al estar próximo a 1, la regresión es significativa, por lo tanto, el modelo está bien ajustado. Esto quiere decir que existe dependencia lineal entre las variables x e y.