R: Análisis de Regresión Lineal

En este apartado, se explicará la función existente en R para obtener modelos de regresión lineal simple.

Ya que aquí sólo se expondrá cómo es el manejo de las funciones, se recomienda que se visite el capítulo: Análisis de Regresión Lineal, para determinar en qué consiste el susodicho método.

Para diseñar modelos de regresión lineal, R, dispone de una función:

R: Análisis de Regresión Lineal.
lm (formula, data, subset, weights, na.action, method = "qr", model = T, x = F, y = F, qr = T, singular.ok = T, contrasts = NULL, offset, ...)	Se utiliza para ajustar modelos lineales.

La función lm() también puede ser utilizada para el análisis de la varianza y análisis de covarianza (aunque la función aov() puede proporcionar una interfaz más conveniente para ellos).

Los argumentos que podemos pasar a la función expuesta anteriormente, son:

• formula: Descripción simbólica del modelo a diseñar.
  

• data: Un marco de datos o lista que contiene las variables en el modelo, es un parámetro opcional,. Si no se define este parámetro, las variables se toman de formula, cuando se ejecuta la función lm().

• subset: Un vector que especifica un subconjunto de las observaciones que se utilizará en el proceso de modelaje. Es un parámetro opcional.

• weights: Un vector de pesos para ser utilizado en el proceso de modelaje. Este parámetro es opcional y debe ser nulo o un vector numérico. Si no es NULL, los mínimos cuadrados ponderados se utiliza con los pesos weights.

• na.action: Le indica a la función lm() que hacer si se encuentra datos del tipo NaN.
  

• method: Método a usar en el modelaje.

• model, x, y, qr: Parámetros lógicos. Si es TRUE los componentes correspondientes del ajuste (x, y o qr) es devuelto.

• contrasts: Una lista opcional.
  

• ... : Argumentos adicionales que se pasa a la regresión en el proceso de modelaje.
  

Para comprobar el funcionamiento de estas funciones, usaremos un ejemplo de aplicación.

Imaginemos el siguiente problema: La tabla de más abajo, presenta los datos sobre el número de cambios de aceite al año (x) y el costo de la reparación (y, en euros) de una muestra aleatoria de 10 coches de una cierta marca y modelo:

x..	3.	5.	2.	3.	1.	4.	6.	4.
y	150	150	250	200	350	200	50	125

Determinar:

a) Ajusta un modelo de regresión lineal simple.

b) ¿Cuánto será el costo de la reparación si el número de cambio de aceite al año es de 5? Utilizar la recta ajustada.

c) Calcula el coeficiente de determinación.

d) Prueba si la regresión es significativa con un nivel de significación de 0.01.

e) Prueba la hipótesis H0: β0 = 0, ¿que conclusiones se puede deducir? Utilizad α = 0.05.

f) Estima los errores estándar de la pendiente y la ordenada en el origen.


Apartado a)

Lo que primero haremos es definir las variables x e y en R:

> x <- c(3, 5, 2, 3, 1, 4, 6, 4)
> y <- c(150, 150, 250, 200, 350, 200, 50, 125)

Si empleamos la función de modelaje de regresión lineal, teniendo en cuenta que la variable de respuesta o dependiente es el costo de la repetición (y):

> lm(y~x)

NOTA: El orden de posicionar las variables es de gran importancia, en este caso, como ya se ha comentado anteriormente, la variable dependiente es el costo de repetición (variable y), por lo que pretendemos una ecuación de regresión ajustada del tipo:

y = b₀ + b₁·x

Donde:

· b₀ y b₁ ≡ Valor numérico de los estimadores β₀ y β₁.

Siguiendo con el ejemplo, R nos devolverá por pantalla:

Call:
lm(formula = y ~ x)

Coefficients:
(Intercept)..............x
....361.81...........-50.69

Llegados a este punto, tenemos ya definido el modelo que mejor se ajusta a los datos ofrecidos por el problema, donde:

· Intercept = b₀, valor numérico del estimador β₀.
· x = b_1, valor numérico del estimador β₁.

Por lo tanto, nuestra recta ajustada es:

y(x) = 361.81 - 50.69·x

Para representar la recta ajustada:

> aceite <- seq(0:length(x))...........# Definimos el eje X
> costo <- 361.81-50.69*aceite.....# Ecuación ajustada
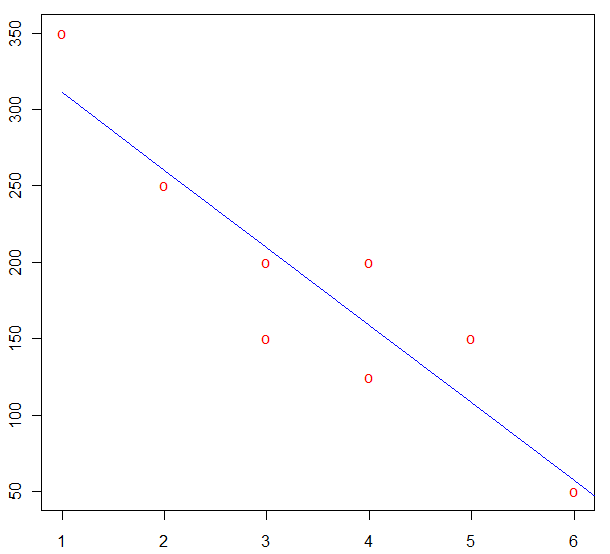
> plot(x, y, pch="o", col=2)
> lines(costo, col=4)

Da como resultado:

El modelo ajustado mediante el método de regresión lineal simple de los datos expuesto en el enunciado del problema.

Bueno, hasta aquí la exposición de cómo obtener los coeficientes de regresión del modelo lineal simple para cualquier estudio de estas características.

Pero esto no acaba aquí, ya que existen varias funciones que conjuntamente con lm(), serán de gran utilidad para realizar un estudio completo de análisis de regresión.

Siguiendo con el ejemplo anterior, almacenaremos los datos ofrecidos por la función lm() en la variable estudio:

> estudio <- lm(y~x)

Y mostraremos varias funciones útiles a usar.

R: Funciones Útiles para Análisis de Regresión Lineal.
coef()	Devuelve los coeficientes del modelo.	> coef(estudio) (Intercept)............. x ..361.80556.. -50.69444
print()	Devuelve un breve resumen del modelo.	> print(estudio) Call: lm(formula = y ~ x) Coefficients: (Intercept)..............x ....361.81...........-50.69

Apartado b)

Una aplicación de ajustar a un modelo de estas características es poder usarlo, posteriormente, para predecir datos, para ello, R dispone a nuestra disposición la función predict():

> predict(estudio)
..........1.................. 2.................3.................4..................5...............6.....................7................8
209.72222....108.33333....260.41667....209.72222....311.11111....159.02778....57.63889....159.02778

Esta función consiste en obtener los posibles datos dados por el modelo teniendo en cuenta la variable dependiente, con una peculiaridad, obtiene todas las posibles predicciones acorde a las posiciones de la variable de predicción (variable x).

Para responder este apartado, tenemos que saber que valor dará el modelo cuando x = 5, en este caso, dicho valor lo encontramos en la posición 2 de la tabla dada por el enunciado, por lo tanto, el valor previsto que ofrece el modelo es: 108.3333.

Lo comprobamos:

y(5) = 361.81 - 50.69·5 = 108.36

Vemos que el resultado no es exactamente el mismo y esto es así porque la función predict() utiliza los coeficientes del modelo con más decimales, en este caso, los dados por la función coef(), la recta, teniendo en cuenta estos valores, es:

y(5) = 361.80556 - 50.69444·5 = 108.33336 ≈ 108.3333

Vemos que depende de la resolución que definamos en R.

Otra función importante y relacionada con predict(), es la residuals(), que nos devuelve el residuo por posición del modelo:

> residuals(estudio)
........... 1..................2..................3...................4..................5...................6...................7................8
-59.722222....41.666667....-10.416667....-9.722222....38.888889....40.972222....-7.638889....-34.027778

Lo comprobamos siguiendo el ejemplo de este apartado, para x = 5 (y = 150):

· Residuo ≡ 150 - 108.3333 = 41.6667

Vemos que coincide perfectamente con lo ofrecido por la función residuals(), teniendo en cuenta la resolución que tengamos definida.


Apartado c), Apartado d), Apartado e) y Apartado f)

Pero seguramente, la forma de obtener un estudio detallado del modelo de regresión, viene de la mano de la función summary():

> summary(estudio)

Call:
lm(formula = y ~ x)

Residuals:
...Min.......1Q......Median....3Q......Max
-59.72..-16.32...-8.68.....39.41...41.67

Coefficients:
......................Estimate....Std.Error....t value....Pr(>|t|)
(Intercept)...361.806.......36.482.......9.917.....6.07e-05 ***
x.................. -50.694.........9.581........-5.291....0.00185 **
---

Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 40.65 on 6 degrees of freedom
Multiple R-squared: 0.8235,.....Adjusted R-squared: 0.7941
F-statistic:...28 on 1 and 6 DF, .p-value: 0.001845

Donde nos encontramos, en los apartados:

· Residuals: Un resumen de los residuos obtenidos por el modelo.

· Coefficients: Un cuadro muy interesante ya que en Estimate, obtenemos los valores de los estimadores, sus errores estándar, y el valor del estadístico y p-valor para las pruebas de hipótesis de los estimadores.

· Residual standard error: El valor del error estándar del residuo.

· Multiple R-squared: Valor del coeficiente de determinación.

· Ajusted R-squared: Valor ajustado del coeficiente de determinación.

Y como respuesta al Apartado c), el coeficiente de determinación es 0.8235.

Para resolver el Apartado d), comprobar si es significativa la regresión, debemos comprobar si la pendiente es cero o no.

Para este estudio deberemos obtener el valor de un estadístico y mediante el estudio de la región crítica o el p-valor, dictaremos, si es significativo el estudio y modelo diseñado.

Todo esto lo realiza R automáticamente mediante el p-valor, para la pendiente, el parámetro t value nos ofrece el valor del estadístico, en este caso: T = -5.291 y a continuación, el valor del p-valor en el parámetro Pr(>|t|), cuyo resultado es 0.00185 y viene con dos asteriscos (**).

Los asteriscos nos informa la frontera del valor de significación para la cual es mayor que el p-valor, lo comprobamos en el apartado Signif. codes.

En nuestro caso, el valor de significación que nos ofrece el enunciado del problema es de 0.01, mayor que el p-valor, por lo que rechazamos la hipótesis nula y aceptamos la alternativa, esto quiere decir que la pendiente no es nula y por ende, la regresión es significativa.

Para resolver el Apartado e), debemos comprobar, mediante pruebas de hipótesis, si el valor de la ordenada es nula o no.

Empleamos un procedimiento similar cuando deducimos si la regresión es significativa en el apartado anterior, el parámetro t value nos ofrece el valor del estadístico, en este caso: T = 9.917 y a continuación, el valor del p-valor en el parámetro Pr(>|t|), cuyo resultado es 0.0000607 y viene con tres asteriscos (***).

Los asteriscos nos informa la frontera del valor de significación para la cual es mayor que el p-valor, lo comprobamos en el apartado Signif. codes.

En nuestro caso, el valor de significación que nos ofrece el enunciado del problema es de 0.05, mayor que el p-valor, por lo que rechazamos la hipótesis nula y aceptamos la alternativa, esto quiere decir que existen evidencias significativas de que el valor de la ordenada en el origen no es nulo.

Y para concluir, Apartado f), los errores estándar de la pendiente la ordenada en el origen vienen ofrecidos en la columna Std. Error:

· Error estándar de la Pendiente: 9.581
· Error estándar de la Ordenada en el Origen: 36.482

---

Como hemos podido comprobar, R dispone de varias funciones que satisfacen cualquier cálculo y operación que se desee realizar sobre el modelo mediante análisis de regresión lineal.

Por supuesto, se recomienda que se emplee la ayuda de R para ampliar conocimientos sobre las funciones expuestas en este capítulo.

> ?lm

Y como conclusión, recordar y aundar en que el análisis de modelos de regresión lineal en R es muy fácil empleando las funciones expuestas en este capítulo como así se ha comprobado.