Problema49: Probabilidad

Ej49. En un estudio sobre enfermedades pulmonares, se ha examinado a 5000 personas de más de 60 años de edad, de los cuales 2000 son fumadoras habituales.

Entre los fumadores 900 tiene alguna afección pulmonar y entre los no fumadores, 750 tiene alguna afección pulmonar.

Si se escoge una persona al azar, determinar la probabilidad de que:

a) Presente afección pulmonar si no fuma.

b) Fume si presenta alguna afección pulmonar.

Si se escogen dos personas, determinar la probabilidad de que:

c) Las dos personas presenten afecciones pulmonares.

d) Sólo una de ellas presente afección pulmonar.


Realizamos una recopilación de datos dados por el enunciado del problema:

· E ≡ 'Fumador habitual'.
· A ≡ 'Afección pulmonar'.

· P(E) = 2000/5000 = 2/5.
· P(Ē) = 3000/5000 = 3/5.

Pasamos a resolver los apartados que nos propone el enunciado del problema.


Apartado a)

Este apartado es introductorio, ya que simplemente tenemos que recopilar los datos que nos ofrece en enunciado.

Nos piden la probabilidad de que presente afección pulmonar si no fuma, ésto es, la probabilidad condicionada. La obtendremos para los dos casos.

· Probabilidad que presente afección pulmonar si no fuma:

Los individuos que componen este grupo, hacen un total de 5000 - 2000 = 3000, teniendo en cuenta que para este grupo tienen una afección pulmonar de 750.

Por lo tanto:

P(A|Ē) = 750/3000 = 1/4

· Probabilidad que presente afección pulmonar si fuma:

Los individuos que componen este grupo, hacen un total de 2000, teniendo en cuenta que para este grupo tienen una afección pulmonar de 900.

Por lo tanto:

P(A|E) = 900/2000 = 9/20

Apartado b)

En esta ocasión, debemos obtener la probabilidad de dado que tenga afección pulmonar, sea fumador, para resolver este apartado, emplearemos la Ley de Bayes:

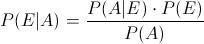
Pero antes, debemos obtener la probabilidad de tener afección pulmonar, para ello, debemos emplear el teorema de la Probabilidad Total:

P(A) = P(A|E)·P(E) + P(A|Ē)·P(Ē) = (9/20)·(2/5) + (1/4)·(3/5) = 33/100

Ahora, estamos en disposición de resolver este apartado, sustituimos valores para obtener la solución:

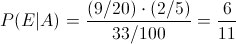
Por lo tanto, la probabilidad de tenga afección pulmonar, sea fumador es de, aproximadamente, 0.545454.


Apartado c)

En este apartado, tenemos que tener en consideración que, ahora, se escogen dos personas al azar.

Y la probabilidad a obtener es la siguiente:

P(A∩A) = P(A)·P(A) = (33/100)·(33/100) = 1089/10000

Por lo tanto, la probabilidad de que dos personas escogidas al azar presente afección pulmonar es de 0.1089, una probabilidad baja.


Apartado d)

Nos piden obtener la probabilidad de que sólo uno presente afección pulmonar:

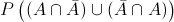
Al ser ambos sucesos independientes, simplificamos:

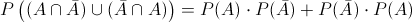
Sustituimos valores y obtenemos la solución a este problema:

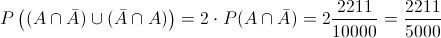
Por lo tanto, la probabilidad de obtener que sólo uno presente afección pulmonar, es de 0.4422.