Ej6. Obtenga la transformada inversa de Laplace de la siguiente función.
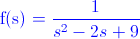
El denominador presenta la siguiente estructura:
a·s2 + b·s + c
Identificamos los elementos:
· a = 1
· b = -2
· c = 9
Podemos completar cuadrados si la agrupamos de la siguiente forma:
a·(s+k)2 + h2
Siendo:
·
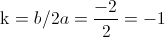
·
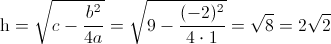
Por lo tanto, la función dada por el enunciado quedará de la siguiente forma:
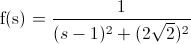
Miramos las tablas y buscamos una transformada que presente similitud a la obtenida, en nuestro caso, la que nos interesa es la que se muestra a continuación.
· Transformada de Laplace de la función: f(t) = eb·x·sin(k·x)
L{eb·x·sin(k·x)} = k/[(s-b)2+k2]
Siendo:
· b = 1.
· k = 2√2.
La antitransformada que debemos obtener es:
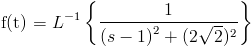
Debemos adaptar la función para que se asemeje a la que queremos obtener:
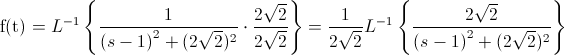
En estos momentos, obtener la transformada inversa es inmediata:
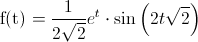
Normalmente, como se suele observar en este problema, para obtener la transformada inversa deberemos manipular la expresión para llegar a una solución adecuada.





0 comentarios:
Publicar un comentario