Problema5: Inversa de Laplace

Ej5. Obtenga la transformada inversa de Laplace de la siguiente función.

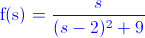
Mirando en las tablas que en este blog se exponen, podemos comprobar a que tipo de función pertenece la dada por el enunciado.

· Transformada de Laplace de la función: f(t) = e^b·x·cos(k·x)

L{e^b·x·cos(k·x)} = (s-b)/[(s-b)²+k²]

Siendo:

· b = 2.
· k = 3.

Por lo tanto, la Antitransformada de Laplace es:

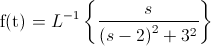
Debemos adaptar la función para que realmente concuerde con la que queremos obtener:

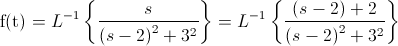
Expandimos la función:

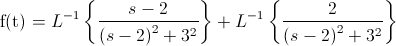
La antitransformada del primer término es inmediata:

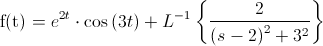
Para el segundo miembro, debemos ver en las tablas a qué función se asemeja, parece fácil ver, que dicha función es:

· Transformada de Laplace de la función: f(t) = e^b·x·sin(k·x)

L{e^b·x·sin(k·x)} = k/[(s-b)²+k²]

Siendo:

· b = 2.
· k = 3.

Por lo tanto, debemos adaptar dicho miembro de la función para que se asemeje al expuesto anteriormente:

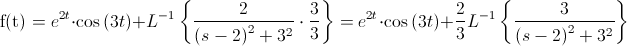
En estos momentos, obtener la transformada inversa es inmediata:

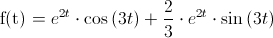
Normalmente, como se suele observar en este problema, para obtener la transformada inversa deberemos manipular la expresión para llegar a una solución adecuada.