Ej79. Un usuario de Internet recibe correos electrónicos en su cuenta personal a una media de 9 correos a la hora. Calcular la probabilidad de que reciba más de 200 correos en un día en su cuenta personal.
Realizamos una recopilación de datos que nos ofrece el enunciado:
· Sea la variable aleatoria X, número de e-mail que recibe en una cuenta personal.
· La variable aleatoria discreta X sigue una distribución Poisson: X ~ P(9) correo/hora.
Tenemos que adaptar nuestro parámetro promedio ya que el estudio está basado en un día (se considera un día igual a 24 horas):
..1....---...9
.24. .---...λ
Por lo tanto, el número medio de correos/día es:
· λ = (9·24)/1 = 216
Debemos obtener la siguiente probabilidad:
Determinaremos, si se puede aproximar a la Normal, para ello, se deben cumplir la siguiente condición:
1. λ > 25 → 216 > 25 OK.
Como podemos comprobar, cumple las restricciones necesarias, por lo que resolveremos este problema usando la aproximación a la normal:
Por lo tanto: X ~ N(λ, √λ) = N(216, √216).
Aplicamos el factor de corrección:
Obtenemos:
Por lo tanto, la probabilidad de que en un día reciba en su cuenta personal de correo electrónico más de 200 e-mail, es de 0.8531.

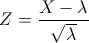
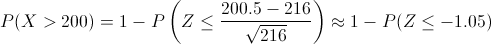




0 comentarios:
Publicar un comentario