Ej78. En una oficina de atención al cliente se organiza una cola. Para analizar la calidad del servicio se coloca un encuestador que entrevista a algunas personas mientras esperan en la cola, de tal forma que elige aleatoriamente a qué personas entrevista con probabilidad de 1/5 de que cada persona sea elegida para ser encuestada.
Se sabe además, que hay el doble de mujeres que de hombres. Para organizar la cola se reparte un número a las personas según van llegando.
Determinar:
a) Cuando han pasado 100 personas por la cola, ¿cuál es la probabilidad de haber encuestado al menos a 15 mujeres?
b) ¿Cuántas personas deben haber pasado como mínimo por la cola para tener una probabilidad de 0.95 de haber realizado al menos 50 encuestas?
Realizamos una recopilación de datos que nos ofrece el enunciado:
· E ≡ 'Persona en la cola que puede ser elegida para ser entrevistada'.
· P(E) = 1/5.
· M ≡ 'Mujeres que esperan en la cola'.
· H ≡ 'Hombres que esperan en la cola'.
Nos dicen que se sabe que hay el doble de mujeres que de hombres.
· P(M) = 2/3.
· P(H) = 1/3.
Pasamos a resolver los distintos apartados que nos ofrece el enunciado del problema.
Apartado a)
· Sea la variable aleatoria X, número de mujeres encuestadas que esperan en la cola.
· Tamaño de la muestra: N = 100 personas.
· La variable aleatoria discreta X sigue una distribución binomial: X ~ B(100, p)
Para obtener la probabilidad de mujeres encuestadas debemos resolver la siguiente probabilidad:
· P(E ∩ M) = P(E)·P(M) = 1/5 · 2/3 = 2/15
· NOTA: Asumimos que los eventos E y M son independientes ya que no tienen relación entre sí.
Por lo tanto:
· La variable aleatoria discreta X sigue una distribución binomial: X ~ B(100, 2/15)
Comprobaremos, si se puede aproximar a la Normal, para ello, se deben cumplir las siguientes condiciones:
1. n·p ≥ 5 → 100·2/15 ≈ 13.333333 ≥ 5 OK.
2. n·q ≥ 5 → 100·(1-2/15) ≈ 86.666667 ≥ 5 OK.
Como podemos comprobar, cumple las restricciones necesarias, por lo que resolveremos este problema usando la aproximación a la normal:
Por lo tanto: X ~ N(n·p, √(n·p·q)) = N(40/3, √104/9).
Debemos obtener la siguiente probabilidad:
Aplicamos el factor de corrección:
Aproximadamente es:
Buscando en la tabla de la Normal, obtenemos la solución a este apartado:
Por lo tanto, la probabilidad de que en una muestra de tamaño 100 personas, se entreviste al menos a 15 mujeres, es de 0.3669.
Apartado b)
En este apartado, debemos definir otro evento:
· Sea la variable aleatoria X, número de encuestas realizadas.
· Tamaño de la muestra: N = n personas.
· La variable aleatoria discreta X sigue una distribución binomial: X ~ B(n, 1/5).
La probabilidad que debemos obtener es la siguiente:
· P(X ≥ 50) = 1 - P(X < 50)
Vamos asumir que la variable aleatoria cumple con las condiciones de poder ser aproximada a la distribución Normal (El número de probabilidad es alto, aunque al terminar el ejercicio deberemos comprobarlo).
Por lo tanto: X ~ N(n·p, √(n·p·q)) = N(n·1/5, √[n·1/5·(1-1/5)]) = N(n/5, √[4n/25)]).
Aplicamos el corrector de continuidad:
· P(X ≥ 50) = 1 - P(X < 50) = 1 - P(X < 49.5)
Tipificamos:
Operamos:
Simplificamos:
En las tablas no disponemos del valor negativo -0.45, pero al estar hablando de la distribución Normal, eso no importa ya que la curva es simétrica. Por lo tanto, buscamos el valor de 0.45 y al resultado final, le añadiremos el carácter negativo.
Es este caso, no está el valor exacto, por lo que realizamos una interpolación lineal:
..1.64.............Z..........1.65
0.4495........0.45.....0.4505
De donde:
1.64 - 1.65.-> 0.4495 - 0.4505
1.64 - Z..-> 0.4495 - 0.45
Calculamos:
Operamos:
Simplificamos:
Resolvemos la ecuación cuadrática y obtenemos dos soluciones:
· n1 ≈ 304.952948
· n2 ≈ 200.871152
¿Cuál de las dos soluciones es válida? En nuestro caso será n1 (~304.952948), ya que es la solución que cumple con todos los pasos que hemos realizado anteriormente en este apartado hasta llegar a la solución.
¿Y por qué tenemos dos soluciones? Pues ya se ha comentado anteriormente algo, es simplemente porque la curva de la Normal es simétrica, esto hace que tengamos dos soluciones: una en su parte derecha y otra en su parte izquierda.
Por lo tanto, las personas que deben de haber pasado como mínimo por la cola para tener una probabilidad de 0.95 de haber realizado al menos 50 encuestas es n > 304 personas.

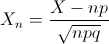
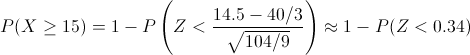
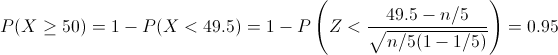
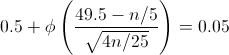
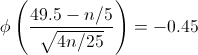
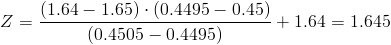
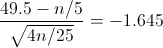




0 comentarios:
Publicar un comentario