Ej90. Los alumnos matriculados en la asignatura Métodos Estadísticos para la Ingeniería de una determinada Escuela de Ingeniería asisten asiduamente a clase en una proporción de 0.6.
Como la asignatura resulta algo complicada de aprobar, diversas academias preparan a los alumnos para superar dicha asignatura, siendo 0.4 la proporción de alumnos que utilizan el servicio de las academias.
Por los resultados obtenidos en convocatorias anteriores, se sabe que los alumnos que asisten tanto a clase como a alguna academia tienen una probabilidad de 0.7 de superar la asignatura, para los alumnos que sólo van a clase, esta probabilidad es de 0.8, para los alumnos que sólo van a alguna academia es de 0.3 y finalmente, los que no acuden ni a clase ni a las academias aprueban con una probabilidad de 0.1.
Se ha previsto que los sucesos para evaluar y realizar un estudio estadístico sobre el comportamiento y el aprobado de los alumnos son:
· E ≡ 'Asistir asiduamente a clase'
· O ≡ 'Acudir a alguna academia'
· A ≡ 'Aprobar la asignatura'
Los sucesos E y O son independientes.
Determinar:
a) Obtener la probabilidad de que un alumno elegido al azar, apruebe la asignatura.
b) Si un alumno ha aprobado la asignatura, hallar la probabilidad de que haya asistido asiduamente a clase.
Realizamos una recopilación de datos dados por el enunciado del problema:
· E ≡ 'Asistir asiduamente a clase'.
· O ≡ 'Acudir a alguna academia'.
· P(E) = 0.6.
· P(O) = 0.4.
· A ≡ 'Aprobar la asignatura'.
· P(A|(E∩O)) = 0.7.
· P(A|(E∩Ō)) = 0.8.
· P(A|(Ē∩O)) = 0.3.
· P(A|(Ē∩Ō)) = 0.1.
Pasamos a resolver los distintos apartados que nos ofrece el enunciado del problema.
Apartado a)
Nos piden obtener la probabilidad de que un alumno elegido al azar, apruebe la asignatura de Métodos Estadísticos para la Ingeniería , para tal fin, emplearemos la Ley de la Probabilidad Total:
Sustituimos valores para obtener la solución a este apartado, teniendo en cuenta que los sucesos E y O son independientes:
Por lo tanto, la probabilidad de que un alumno elegido al azar apruebe la asignatura de Métodos Estadísticos para la Ingeniería es de 0.528.
Apartado b)
Nos piden obtener la probabilidad de que dad0 que un alumno apruebe la asignatura, éste asista asiduamente a clase, emplearemos para tal fin la Ley de Bayes:
Sustituimos valores, teniendo en cuenta que los sucesos E y O son independientes, para obtener el resultado a este apartado:
Por lo tanto, la probabilidad de dado que un alumno apruebe éste asista asiduamente a clase es de, aproximadamente 0.863636.

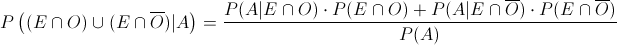
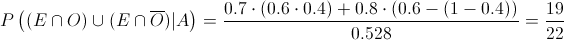




0 comentarios:
Publicar un comentario