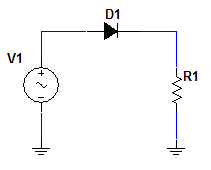
En esta ficha vamos a estudiar el Rectificador de Media Onda: Carga Resistiva. Básicamente consiste en un circuito con una fuente alterna de entrada, un conmutador (en este caso emplearemos un diodo) y una resistencia, se suelen asociar al apartado de rectificadores no controlados.
Los objetivos principales que buscamos son:
- Análisis de circuitos de este tipo.
- Obtención de expresiones matemáticas finales que definan este tipo de circuitos.
- Obtención de gráficas de tensión e intensidad (si se requieren) para posterior análisis.
Breve descripción del funcionamiento del circuito:
· Semiciclo Positivo: El diodo estará en conducción y por lo tanto, la tensión de salida será distinta mayor de cero (La tensión de R1 seguirá a la tensión de entrada V1).
· Semiciclo Negativo: El diodo estará en corte y por lo tanto, la tensión de salida será cero.
Al estar presente un diodo, podemos escoger entre cualquiera de los modelos: Modelo ideal, 1ª Aproximación o 2ª Aproximación. En la mayoría de los casos (y más en el ámbito de la electrónica de potencia, es aconsejable emplear los modelos ideales ya que el error que se cometerá será muy bajo).
Pero en nuestro caso, al ser éste una ficha de estudio, vamos a emplear la 2ªAproximación y de ésta obtendremos las ecuaciones matemáticas de los modelos inferiores. ¡Manos a la obra! Estudiaremos ambos semiciclos por separado.
· Semiciclo Positivo.
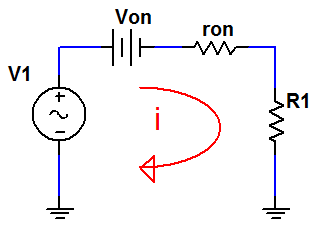
Esto quiere decir que la tensión de entrada es positiva, el diodo está en estado de conducción y el circuito equivalente (empleando la 2ª Aproximación del diodo) es el que se muestra a continuación:
Resolvemos la maya en la dirección que se muestra en la figura obteniendo la siguiente expresión:
-V1 + i·ron + Von + i·R1 = 0
Agrupamos:
i·(ron + R1) = V1 - Von
Despejamos:
Pues ya está resuelto, si tenemos en cuenta que la mayoría de veces la fuente de entrada es del tipo sinusoidal cómo:
· V1 = Vm·sen(wt), siendo Vm la amplitud en RMS (valor eficaz).
Pues tenemos la siguiente solución:
Para obtener la tensión en la carga simplemente utilizaríamos la Ley de Ohm (V = I·R).
· Semiciclo Negativo.
En este semiciclo, la tensión de entrada es inferior a las necesarias para que el diodo esté en conducción por lo tanto, el diodo está en corte y no existe corriente circulando por el circuito.
· i(t) = 0
· VR1 = 0
El estudio no debe concluir aquí, ya que debemos exponer (de forma clara) las condiciones de cambio de estado del diodo y así de esta manera, obtener los límites de funcionamiento.
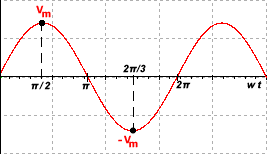
La onda de entrada (V1) debe presentar la siguiente forma (forma senoidal):
Con los resultados obtenidos anteriormente, vamos a calcular las condiciones en las cuales el diodo está en conducción y en corte.
· Condiciones: Diodo en Conducción.
Teniendo en cuenta que estamos trabajando con la 2ªAproximación del diodo, se deben cumplir ciertas condiciones para que el diodo esté en conducción.
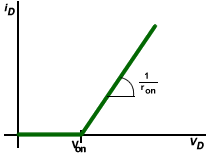 | Condiciones: | |
| · VD ≥ Von + iD·ron | ||
| · iD > 0 | ||
De manera gráfica, podemos observar que para que el diodo esté en conducción se debe cumplir: VD > Von
De manera analítica lo podemos demostrar, despejamos de la primera iD condición:
· iD ≤ (VD -Von)/ron
Teniendo en cuenta la segunda condición, llegamos a la conclusión que hicimos de manera gráfica: VD > Von.
Muy bien, pero ese resultado sólo nos explica las condiciones del diodo, lo que nos interesa es dar, de manera analítica, el ángulo (wt) exacto dónde el diodo pase del estado de conducción a corte. Realizando un análisis (mediante malla) de la tensiones de los elementos del circuito obtenemos lo siguiente:
· VD = Vi -VR1
Teniendo en cuenta la condición del diodo en conducción:
· VD = Vi -VR1 ≥ Von + iD·ron
Despejamos el parámetro de la intensidad:
Teniendo en cuenta que la intensidad, para que el diodo esté en conducción, debe ser positiva llegamos a la siguiente condición:
Si prestamos atención en la expresión anterior, la única relación que puede violar la condición obtenida, es la siguiente (y de la manera en la que se expresa):
· Vm·sen(wt) - Von ≤ 0
Si dicha expresión es menor o igual a cero, el diodo estará en corte. Para esta condición, que el diodo entre en corte, vamos a realizar el siguiente cambio de variable para el ángulo:
· β = wt
Por lo tanto, para que el diodo pase de conducción a corte se debe dar la siguiente condición:
· Vm·sen(β) - Von ≤ 0
Despejamos el ángulo de extinción o cambio de estado (β):
Para éste ángulo, el diodo cambiará de estado. Pero necesitamos saber en qué momento preciso va a ocurrir, para ello, vamos analizar los puntos críticos de la onda de entrada (V1), éstos son dónde dicha onda pase por cero, tendremos que hacer un análisis pivotando entre dichos puntos.
· wt = 0
El diodo no entrará en conducción justamente cuando empieza el semiciclo positivo de la onda de entrada, sino que se deben cumplir las condiciones puestas anteriormente.
· Vm·sen(β1 - wt) - Von ≤ 0
Despejamos:
· wt = π
El diodo no estará en corte justamente cuando empieza el semiciclo negativo de la onda de entrada, ya que entrará antes por las condiciones anteriores expuestas.
· Vm·sen(wt - β2) - Von ≤ 0
Despejamos:
· wt = 2π
El análisis es el mismo que el realizado cuándo wt = 0. Tenemos la siguiente expresión:
· Vm·sen(β3 - wt) - Von ≤ 0
Despejamos:
Habiendo realizado un análisis con la 2ªAproximación del diodo, es fácil obtener las expresiones del modelo ideal y de la 1ªAproximación. Se muestra en la siguiente tabla las expresiones para cada tipo de modelo y análisis para el circuito rectificador de media onda no controlado con carga resistiva:
| Modelo Ideal | 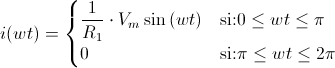 |
| Modelo 1ªAproximación | 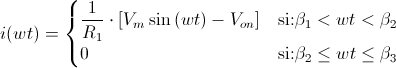 |
| Modelo 2ªAproximación | 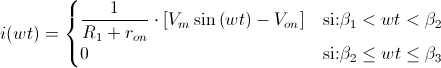 |
Dónde:
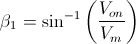
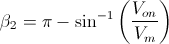
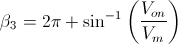
Llegados a este punto, hemos identificado, analizado y obtenido las expresiones matemáticas necesarias para este tipo de circuitos, ahora, nos falta aportar, de manera gráfica, el resultado en forma de tensión (entrada contra salida).
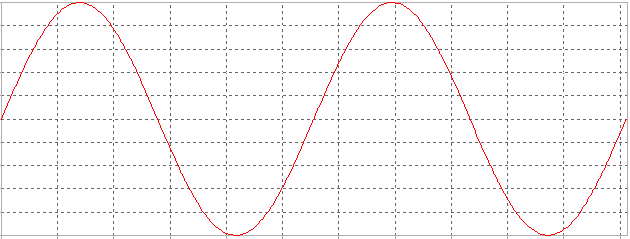
Para este tipo de circuitos: Rectificador No Controlado Media Onda: Carga Resistiva, las gráficas de tensión son las que se muestran a continuación:
| Tensión de entrada: Vs |
 |
| Tensión de salida: Vo |
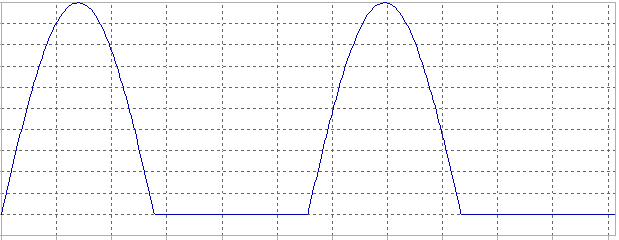 |
Como podemos observar en las ondas de salida, el circuito se comporta tal y cómo hemos realizado el estudio previo, sólo actuando en el semiciclo positivo.
Por último, se facilita scripts (o programas) para distintas plataformas dónde poder obtener los cálculos necesarios para este tipo de circuito de manera automática:
| --En Construcción-- |
|---|
| --- |
| --- |
También os podéis descargar el circuito estudiado en esta ficha para que lo simuléis vosotros mismos:
 |  | Rectificador No Controlado Media Onda: Carga Resistiva |
 |  | Rectificador No Controlado Media Onda: Carga Resistiva |
Acabaremos esta ficha con una conclusión, el estudio de este tipo de circuitos no es (relativamente) complicado y en cambio, es un ejercicio muy útil para adentrarse en el manejo de dispositivos como diodos y su interacción con el tipo de señales de onda de entrada.

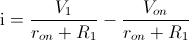
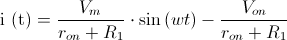
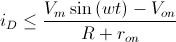
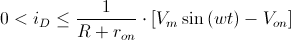
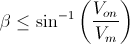
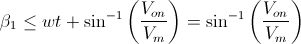
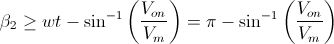
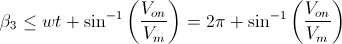




0 comentarios:
Publicar un comentario