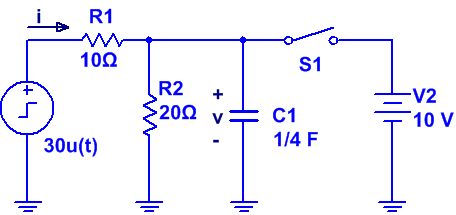
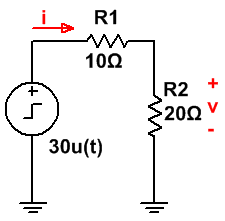
Ej4. El interruptor que se muestra en el siguiente circuito, ha estado cerrado durante un largo período de tiempo. En t = 0, el interruptor se abre.
Obtener:
a) El valor de v(t) e i(t).
b) La constante de tiempo del circuito.
Apartado a)
En este apartado nos piden obtener el valor de v(t) que se muestra en el enunciado del problema, para el ello, debemos prestar atención a las condiciones que nos expone el enunciado.
· Interruptor ha estado cerrado por un largo período de tiempo: Esto significa que el condensador se ha cargado completamente y antes de abrir el interruptor (en t = 0), su comportamiento es como un circuito abierto.
Por otro lado, una de las fuentes de tensión del circuito (la que está más a la izquierda) se comporta cómo una función escalón, cuya definición es:
Una vez tenemos clara las condiciones del problema, vamos a abordarlo teniendo en cuenta la posición del interruptor.
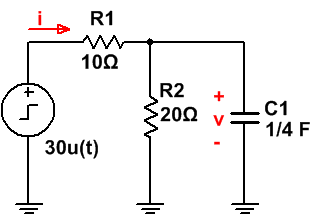
· Interruptor Cerrado (t < 0):
Como ya hemos mencionado, al estar el interruptor un largo período de tiempo cerrado, el condensador se comporta como un circuito abierto. Aparte, por la propia definición de la función escalón, en este instante de estudio (t < 0), u(t) = 0.
El circuito que tenemos es el siguiente:
Vamos a calcular la tensión inicial del condensador, en este caso es fácil, ya que todos los elementos están en paralelo:
· v(0-) = 10 V
Esto quiere decir que, estando el interruptor cerrado y habiéndose mantenido durante un largo período de tiempo, el condensador tendrá una tensión de 10 V.
Obtener la intensidad i, también es fácil:
· i(0-) = - 10/10 = - 1 A
Por lo tanto, la corriente i cuando el interruptor ha estado cerrado por un largo período de tiempo es de - 1 A.
· Interruptor Abierto (t = 0):
El circuito que tenemos es el siguiente:
Para realizar el análisis hay que tener en cuenta que el condensador tiene una tensión inicial (obtenida cuando el interruptor estaba cerrado por un largo período de tiempo) y la función escalón es u(t = 0) = 30 V.
Para este caso, tenemos dos comportamiento en el circuito, por un lado: El régimen transitorio (vn) y por el otro: El régimen permanente (vp). La solución general será del tipo:
· v(0+) = vp + vn
Así que vamos a obtener los dos por separado.
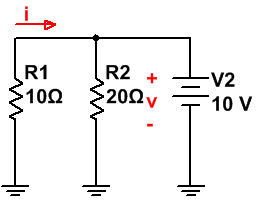
· Régimen Permanente:
Este caso, el interruptor abierto durante un largo período de tiempo, por lo que, el condensador se cargará completamente y se comportará como un circuito abierto.
El circuito que tenemos es el siguiente:
Obtener la tensión del condensador es fácil, simplemente con un divisor de tensión:
· vp = 30·[20/(20 + 10)] = 20 V.
El condensador se cargará hasta la tensión máxima que proporciona el circuito, en este caso, hasta 20 V.
· Régimen Transitorio:
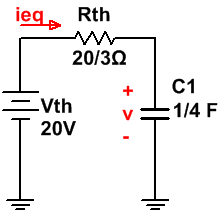
El condensador se está cargando, en este caso, vamos a obtener el circuito equivalente de Thevenin, por su sencillez y sobre todo porque, nos simplificará los cálculos posteriormente.
| ==> | 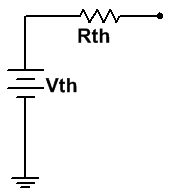 |
Si realizamos los cálculos, obtenemos el valor de los parámetros deseados:
· VTh = 20 V.
· RTh = (20/3) Ω
El circuito que tenemos es el siguiente:
Realizamos el análisis mediante LVK (teniendo en cuenta que el condensador tiene una tensión inicial de 10 V y la fuente de tensión equivalente de Thevenin es de 20 V, la corriente circulará tal y cómo se indica en la figura del circuito anterior):
· [Ec1] vn + ic·RTh - VTh = 0
Dónde:
· ic = C·Dvn
Sustituimos el valor en [Ec1] y dividimos por C:
· Dvn + [1/(RTh·C)]·vn = VTh/(RTh·C)
Ya tenemos nuestra ecuación diferencial de 1º Orden, la ecuación homogénea es:
· [Ec2] Dvn + [1/(RTh·C)]·vn = 0
Por teoría, sabemos que una solución a la ecuación diferencial homogénea de 1º Orden es:
· vn(t) = k·e-A·t
Realizamos la primera derivada y sustituimos en [Ec2]:
- k·A·e-A·t + [1/(RTh·C)]·k·e-A·t = 0
Analizamos en circuito en el instante t = 0 (el interruptor se abre), por lo tanto:
- k·A + [1/(RTh·C)]·k = 0
Despejamos el parámetro A:
· A = 1/(RTh·C) = 1/[(20/3)·(1/4)] = 0.6 s-1
Una vez obtenido el parámetro A, vamos a obtener el valor del parámetro k, para ello, aplicamos la condición del condensador.
· Condensador: La tensión no puede cambiar bruscamente en un instante concreto.
En el instante t = 0:
· v(0-) = v(0+)
Por lo tanto:
· 10 = vp + vn = 20 + k·e-0.6·t = {t = 0} = 20 + k
Despejamos k:
· k = 10 - 20 = - 10
Así que, una expresión para la tensión del condensador es:
· v(t) = 20 - 10·e-0.6·t , t ≥ 0
Una vez que tenemos la tensión del condensador, es fácil obtener la corriente que nos piden, realizamos un análisis de LVK:
· - 30 + i(t)·10 + 20 - 10·e-0.6·t = 0
Despejamos el parámetro que nos piden:
· i(t) = 1 + e-0.6·t, t ≥ 0
En modo de conclusión, la tensión del parámetro v(t) que nos indica el enunciado del problema tendrá la siguiente expresión matemática:
Cuya representación gráfica es la que se muestra a continuación:
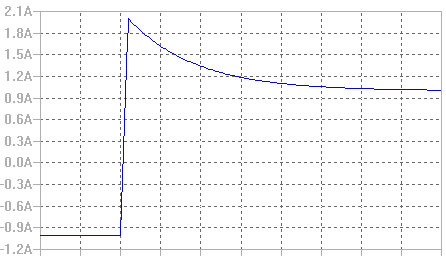
Y para la corriente que nos indica el enunciado del problema:
Cuya representación gráfica es la que se muestra a continuación:
Como podemos ver en la gráfica (y en la expresión matemática de la corriente obtenida anteriormente), en el instante t = 0, la corriente pasa de valer -1 a 2 A.
Apartado b)
En este caso, obtener la constante de tiempo es bastante fácil:
· τ = 1/A = 1/0.6 ≈ 1.666667 s
Por lo tanto, la constante de tiempo es, aproximadamente, 1.67 s.
Os dejo una simulación realizada en LTSpice:
| Problema 4: Transitorios de 1º Orden | |||||||||
|
La simulación no es fiel a las especificaciones del problema, ya que, entre otras cosas, simular un interruptor en LTSpice es algo complicado. Aún así, se puede ver perfectamente cómo evoluciona la tensión del condensador y la corriente del circuito y obtener la constante de tiempo del circuito.


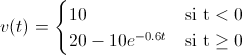

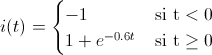








0 comentarios:
Publicar un comentario