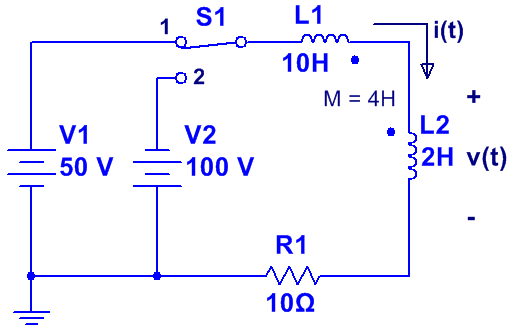
Ej8. El circuito de la figura está en régimen permanente con el interruptor en la posición 1. En t = 0, el interruptor pasa al terminal 2.
Obtener:
a) La evolución de i(t).
b) La evolución de v(t).
Apartado a)
En este apartado, nos piden obtener el valor de i(t) que se muestra en el circuito del problema, para el ello, debemos prestar atención a las condiciones que nos expone el enunciado.
· El circuito está en régimen permanente cuando el interruptor está en la posición 1: Esto quiere decir que ambos inductores están cargados completamente y por ende, se comportan como corto circuito.
Como en un instante determinado (en t = 0), el circuito cambia su composición debido al interruptor, vamos a estudiar el circuito en cada instante de cambio.
· t < 0. S posición 1:
Según el enunciado, el interruptor ha estado en esta posición durante un largo período de tiempo, por lo que solamente tenemos régimen permanente. Esto quiere decir que los inductores se habrán cargado completamente y su comportamiento es de corto circuito.
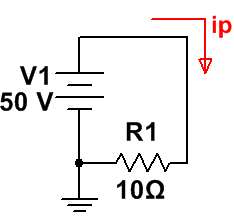
El circuito que tendremos será el siguiente:
Obtener la intensidad es directo:
· ip = 50/10 = 5 A
Esto quiere decir, que estando el interruptor en la posición indicada anteriormente y mediante un largo período de tiempo, la intensidad, en bornas, de ambos inductores será de 5 A.
Ahora, pasamos a estudiar que ocurre cuando el interruptor pasa a la posición 2.
· t = 0. S posición 2:
En este instante y circunstancias, tenemos el siguiente circuito:
Aparte, debemos tener en cuenta que el inductor equivalente cuenta con una corriente inicial de:
· i(0-) = 5 A
Para este caso, tenemos dos comportamiento en el circuito, por un lado: El régimen transitorio (in) y por el otro: El régimen permanente (ip). La solución general será del tipo:
· i(0+) = ip + in
Así que vamos a obtener los dos, por separado.
· Régimen Permanente:
Este caso, el interruptor S1 permanece en la posición 2 durante un largo período de tiempo, por lo que, ambos inductores se cargarán completamente y se comportarán como un corto circuito.
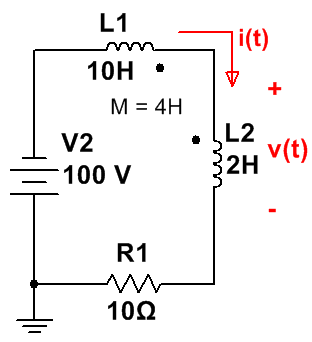
El circuito que tenemos es el siguiente:
Obtener la corriente es fácil:
· ip = - 100/10 = - 10 A.
El inductor equivalente se cargará hasta la intensidad máxima que proporciona el circuito, en este caso, hasta - 10 A.
· Régimen Transitorio:
El inductor equivalente se está cargando, el circuito que tenemos es el siguiente:
Como se puede apreciar en la anterior figura, ambos inductores están acoplados magnéticamente. Sus tensiones, teniendo en cuenta los criterios de signos, son:
· uL1(t) = - (- L1Di1 + M12Di2) = L1Di1 - M12Di2
· uL2(t) = - M21Di1 + L2Di2
Siendo:
· M21= M12
· i1 = i2 = in
Realizamos el análisis mediante LVK:
· [Ec1] 100 + 10Din + 2Din + 10in - (2·4)Din= 0
Agrupamos:
· 4Din + 10in = - 100
Dividimos por 4:
· Din + (5/2)in = - 25
Ya tenemos nuestra ecuación diferencial de 1º Orden, la ecuación homogénea es:
· [Ec2] Din + (5/2)in = 0
Por teoría, sabemos que una solución a la ecuación diferencial homogénea de 1º Orden es:
· in(t) = k·e-A·t
Realizamos la primera derivada y sustituimos en [Ec2]:
- k·A·e-A·t + (5/2)·k·e-A·t = 0
Analizamos en circuito en el instante t = 0, por lo tanto:
- k·A + (5/2)·k = 0
Despejamos el parámetro A:
· A = 5/2 = 2.5 s-1
Por lo tanto, la constante de tiempo en el instante t = 0 es:
· τ = 1/A = 1/2.5 = 0.4 s
Una vez obtenido el parámetro A, vamos a obtener el valor del parámetro k, para ello, aplicamos la condición del condensador.
· Inductor: La corriente no puede cambiar bruscamente en un instante concreto.
Hay que tener en cuenta que el inductor equivalente presenta una carga de corriente entre sus bornas en este instante de tiempo:
· i(0-) = 5 A
En el instante t = 0:
· i(0-) = i(0+)
Por lo tanto:
· 5 = ip + in = - 10 + k·e-(5/2)·t = {t = 0} = - 10 + k
Despejamos k:
· k = 5 + 10 = 15
Así que, una expresión para la corriente que nos dicta el enunciado del problema es:
· i(t) = - 10 + 15·e-(5/2)·t , t ≥ 0
En modo de conclusión, la corriente del parámetro i(t) que nos indica el enunciado del problema tendrá la siguiente expresión matemática:
Cuya representación gráfica es la que se muestra a continuación:
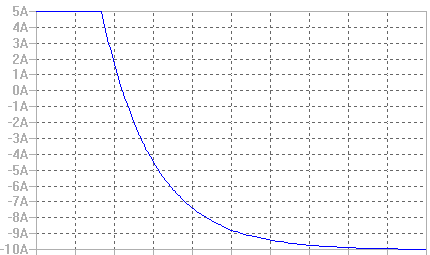
Apartado b)
En este apartado nos piden obtener la evolución de la tensión del segundo inductor (L2), por propia definición, sabemos que la tensión de un inductor viene expresado por la siguiente expresión matemática:
· u(t) = Leq·DiL2(t)
· NOTA: ¡Cuidado! Ya que este inductor está acoplado magnéticamente, por lo que su inductancia será (teniendo en cuenta los criterios de signos):
· Leq = L2 - M12 = 2 - 4 = - 2 H
Dónde tenemos ya calculado la corriente que atraviesa a dicho inductor (obtenida en el apartado anterior):
· iL2(t) = i(t)
Por lo tanto, simplemente, realizamos la derivada para obtener la solución a este apartado:
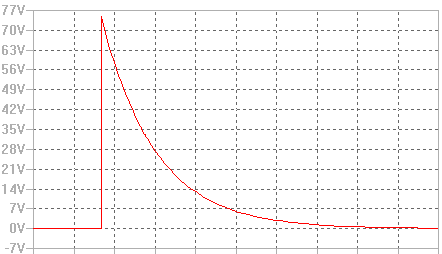
Cuya representación gráfica es la que se muestra a continuación:
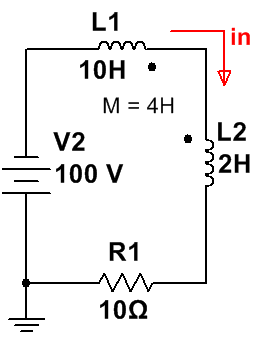
Os dejo una simulación realizada en LTSpice:
| Problema 8: Transitorios de 1º Orden | |||||||||
|
La simulación no es fiel a las especificaciones del problema, ya que, entre otras cosas, simular un interruptor en LTSpice es algo complicado. Aún así, se puede ver perfectamente cómo evoluciona la corriente y obtener la constante de tiempo del circuito.



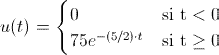








0 comentarios:
Publicar un comentario