En este capitulo analizaremos los circuitos llamados de 1º Orden, son aquellos en los que podemos encontrar Resistores y Bobinas o Condensadores, generalmente, podemos clasificarlos de dos maneras:
· Circuitos de Primer Orden Sin Fuentes de Excitación: Son aquellos circuitos dónde no encontramos ninguna fuente de excitación (ya sea de intensidad o de tensión).
· Circuitos de Primer Orden Con Fuentes de Excitación: Son aquellos circuitos dónde podemos encontrar fuentes de excitación (ya sea de tensión o intensidad).
Ejemplos concretos los vamos a encontrar en la parte de problemas dedicados a este capitulo, por lo que vamos a exponer de manera matemática (es decir, general), la forma de abordar este tipo de circuitos.
Para empezar, se le denominado circuitos de 1º Orden ya que la ecuación que define el comportamiento del circuito es una ecuación diferencial de 1º Orden, suele ser del tipo siguiente:
Dónde:
· f(t) ≡ Es la respuesta o variable que deseamos calcular.
· A ≡ Es una constante, siendo su inversa la llamada constante de tiempo (τ = 1/A).
· eg(t) ≡ La excitación (generalmente, será una función temporal).
Este tipo de ecuaciones (ecuación diferencial de 1º Orden), tiene una solución completa de la siguiente forma:
Como podemos ver, la solución tiene dos partes, una es la solución de la ecuación homogénea (fh) y la otra, es la solución particular (fp) también llamada la respuesta forzada y es del mismo tipo que la excitación.
Para obtener una solución a la respuesta homogénea, debemos obtener la solución a la ecuación diferencial homogénea:
Donde sabemos que existe una solución llamada: respuesta natural o transitoria, del tipo siguiente:
· fh(t) = k·e-At
Bien, para obtener tanto la constante k cómo la A, debemos aplicar las condiciones iniciales del problema que estemos resolviendo (por ejemplo, que la bobina o el condensador esté cargado con una cierta carga inicial o no).
· NOTA: Se ha empleado el operador D en la realización de los ejercicios para mejorar la comodidad y claridad de las expresiones matemáticas.
Donde:
· D ≡ d/dt
Entraremos en más profundidad en los siguientes problemas:
| Problemas: Circuitos de 1º Orden | |
| Problema 1 | Problema 11 |
| Problema 2 | Problema 12 |
| Problema 3 | Problema 13 |
| Problema 4 | Problema 14 |
| Problema 5 | Problema 15 |
| Problema 6 | Problema 16 |
| Problema 7 | Problema 17 |
| Problema 8 | Problema 18 |
| Problema 9 | Problema 19 |
| Problema 10 | Problema 20 |
El enunciado de los siguientes problemas serán con Amplificadores Operacionales:
| Problemas: Circuitos de 1º Orden ( Con AMPLIFICADORES OPERACIONALES ) | |
| Problema 1 | Problema 11 |
| Problema 2 | Problema 12 |
| Problema 3 | Problema 13 |
| Problema 4 | Problema 14 |
| Problema 5 | Problema 15 |
| Problema 6 | Problema 16 |
| Problema 7 | Problema 17 |
| Problema 8 | Problema 18 |
| Problema 9 | Problema 19 |
| Problema 10 | Problema 20 |
· NOTA: Para obtener la solución a este tipo de circuitos, podemos resolverla ecuación diferencial (tal y cómo se ha explicado, de manera general, anteriormente) o, emplear la transformada de Laplace.
También es interesante emplear calculadoras o software matemático (tipo Maxima, Maple, Matlab, etc) para obtener la solución más rápidamente.

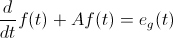
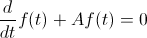




0 comentarios:
Publicar un comentario