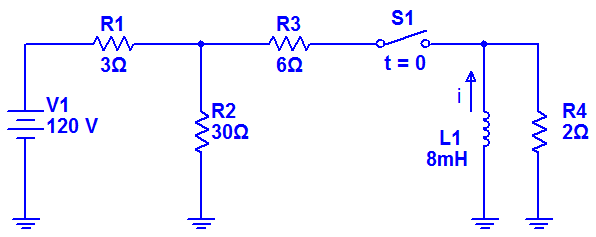
Ej1. El interruptor que se muestra en el siguiente circuito ha permanecido cerrado durante un largo período de tiempo, y es abierto en el instante t = 0.
Obtener:
a) El valor inicial de i.
b) La energía inicial almacenada en el inductor.
c) ¿Cuál es la constante de tiempo del circuito para t > 0?
d) La expresión de i para t ≥ 0.
e) ¿Cuál es el porcentaje de energía inicial que ha sido disipada en el resistor de 2 Ω pasados 5 ms de que el interruptor fue abierto?
Apartado a)
En este apartado nos piden obtener la intensidad inicial, donde el circuito estuvo con el interruptor cerrado durante un período de tiempo largo.
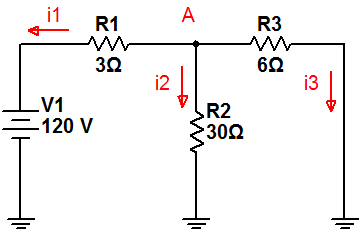
El circuito equivalente a esta situación es:
Vamos a obtener el valor de la tensión del nodo A:
· Nodo A: (VA - 120)/3 + VA/30 + VA/6 = 0
Agrupamos:
· VA·(1/3 + 1/30 + 1/6) = 120/3
Y despejamos para obtener el valor de la tensión del nodo A:
· VA = 75 V.
Ahora, es fácil obtener el valor que nos piden (valor de la intensidad en régimen permanente a través del inductor):
· i = - i3 = - 75/6 = - 12.5 A
Apartado b)
En este apartado debemos obtener el valor de la energía inicial (cuando el inductor está en régimen permanente), almacenada en el inductor. Para ello, aplicamos su expresión matemática:
· w(0) = (1/2)·L·i2 = (1/2)·8·10-3·(-12.5)2 = 625 mJ
Apartado c)
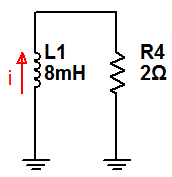
En este apartado, el interruptor se abre, por lo que el circuito que tenemos es el siguiente:
Tal como está es fácil (por teoría) obtener la constante de tiempo del circuito, aún así, aquí vamos a obtenerla resolviendo el circuito.
Haciendo un análisis obtenemos la siguiente ecuación:
· L·DiL - iR·R = 0
Hay que tener en cuenta que la intensidad del inductor es la misma que atraviesa al resistor (iR = - iL), dividimos por L y tenemos:
· [Ec1] DiL + iL·(R/L) = 0
Obtenemos una ecuación diferencia de 1º orden homogénea donde, por teoría, sabemos que una solución es:
· iL(t) = k·e-A·t
Realizamos la primera derivada y sustituimos en [Ec1]:
- k·A·e-A·t + (R/L)·k·e-A·t = 0
El interruptor se abre en el instante t = 0, por lo tanto:
- k·A + (R/L)·k = 0
Sustituimos el parámetro A:
· A = R/L
Por lo tanto, la constante de tiempo y la solución a este apartado es:
· τ = 1/A = L/R = (8·10-3)/2 = 4 ms
Apartado d)
En este apartado nos piden obtener una expresión para la corriente que atraviesa al inductor. Ya tenemos la mitad del camino hecho en el apartado anterior.
Nos falta obtener el valor del parámetro k, para ello, aplicamos la condición del inductor.
· Inductor: La corriente no puede cambiar bruscamente en un instante concreto.
En el instante t = 0:
· i(0-) = i(0+)
Por lo tanto:
-12.5 = k·e-(R/L)·0
Obtenemos el valor del parámetro que nos faltaba:
· k = - 12.5
Así que, una expresión para la corriente que atraviesa el inductor será:
· iL(t) = - 12.5·e-250·t , t ≥ 0
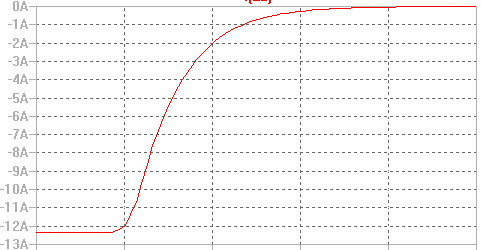
Gráficamente, la corriente que atraviesa al inductor se muestra en la siguiente figura:
Apartado e)
En este apartado nos piden el porcentaje de energía inicial que ha sido disipada en el resistor de 2 Ω pasados 5 ms de que el interruptor haya sido abierto, por definición, la energía es:
Dónde:
· pR = vR·iR = [vR = R·iR] = R·i2R
Para este caso, iR = iL y t = 5 ms, sustituimos y resolvemos la integral:
Ya tenemos la energía disipada por el resistor pasados 5 ms de estar el interruptor cerrado, pero este apartado nos piden el porcentaje de energía disipada respecto a la inicial.
La energía inicial ya la hemos calculado anteriormente (Apartado b)), por lo que la solución a este apartado es:
· [0.573697/0.625]·100 = 91.79152
Por lo tanto, el porcentaje de energía inicial que ha sido disipada en el resistor de 2 Ω pasados 5 ms de que el interruptor se cerrara es de, aproximadamente, 91.79%.
Os dejo una simulación realizada en LTSpice:
| Problema 1: Transitorios de 1º Orden | |||||||||
|
La simulación no es fiel a las especificaciones del problema, ya que, entre otras cosas, simular un interruptor en LTSpice es algo complicado.
Aún así, se puede ver perfectamente cómo evoluciona la intensidad a través del inductor.


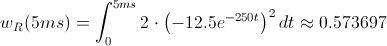








0 comentarios:
Publicar un comentario