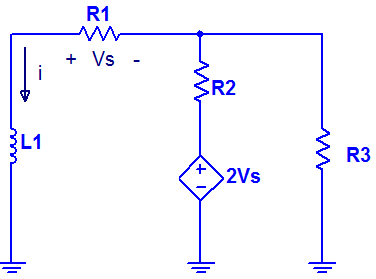
Ej2. Dado el siguiente circuito:
Dónde los valores de los componentes que lo componen son:
· L = 1/6 H.
· R1 = 3 Ω.
· R2 = 1 Ω.
· R3 = 5 Ω.
Aparte, se sabe que la bobina tiene una carga inicial, en el instante t = 0, de 5 A. Obtener:
a) El valor de i.
b) El valor de Vs.
c) La constante de tiempo del circuito.
Apartado a)
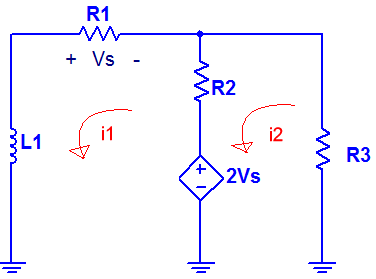
En este apartado nos piden obtener el valor de i que se muestra en el enunciado del problema, para el ello, vamos a emplear el método de mallas.
Se pueden diferenciar, claramente, dos mallas, realizamos el análisis y obtenemos las expresiones a cada malla:
· [Malla 1] i1·(R1 + R2) + LDi1 - i2·R2 = 2Vs
· [Malla 2] - i1·R2 + i2·(R2 + R3) = - 2Vs
De la ecuación de [Malla 2], despejamos entorno a la corriente i2:
· i2= (i1·R2 - 2Vs)/(R2 + R3)
Ahora, simplemente sustituimos dicho valor, en la ecuación de [Malla 1] y agrupamos:
Ya tenemos nuestra ecuación diferencial de 1º Orden, pero hay que tener en cuenta que el valor de Vs es de una fuente dependiente de tensión, cuyo valor es:
· Vs= - i1·R1
Por lo tanto, sustituimos y dividimos por L en nuestra ecuación diferencial de 1º Orden:
Simplificamos:
· [Ec1]:
Por teoría, sabemos que una solución a la ecuación diferencial homogénea de 1º Orden es:
· i1(t) = k·e-A·t
Realizamos la primera derivada y sustituimos en [Ec1]:
- k·A·e-A·t + [(R2·R3 + 3R1·R3 + R1·R2)/(L·(R3+ R2))]·k·e-A·t = 0
Analizamos en circuito en el instante t = 0 (el enunciado del problema, nos indica éste punto de partida dándonos una carga inicial del inductor), por lo tanto:
- k·A + [(R2·R3 + 3R1·R3 + R1·R2)/(L·(R3+ R2))]·k = 0
Despejamos el parámetro A:
· A = [(R2·R3 + 3R1·R3 + R1·R2)/(L·(R3+ R2))]
Una vez obtenido el parámetro A, vamos a obtener el valor del parámetro k, para ello, aplicamos la condición del inductor.
· Inductor: La corriente no puede cambiar bruscamente en un instante concreto.
En el instante t = 0:
· i(0-) = i(0+)
Por lo tanto (teniendo en cuenta que en este circuito sólo está presente el régimen transitorio):
5 = k·e-A·0
Obtenemos el valor del parámetro que nos faltaba:
· k = 5
Así que, una expresión para la corriente que atraviesa el inductor será:
Ya que tenemos la expresión de la corriente que nos pide el enunciado del problema de manera simbólica, vamos a sustituir por los valores de cada componente, obteniendo la solución a este apartado:
· i = i1(t) = 5·e-53·t , t ≥ 0
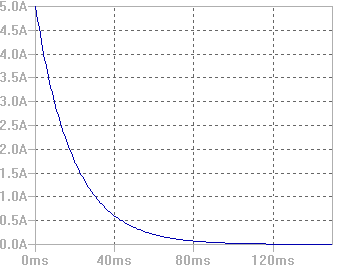
Una representación gráfica de cómo se comporta dicha intensidad, se muestra en la siguiente figura:
Apartado b)
En este apartado, nos piden obtener el valor de la tensión Vs, en este caso, es fácil obtenerla ya que tenemos el valor de la intensidad calculada en el apartado anterior.
Por lo tanto:
· Vs = - i·R1
Sustituimos valores:
· Vs = - 5·e-53·t·3 = - 15·e-53·t , t ≥ 0
Una representación gráfica de cómo se comporta dicha tensión, se muestra en la siguiente figura:
Apartado c)
Tenemos todo lo necesario ya calculado por lo que, la constante de tiempo y la solución a este apartado es:
· τ = 1/A = (L·(R3+ R2))/(R2·R3 + 3R1·R3 + R1·R2) = (1/6·(5+1))/(1·5+3·3·5+3·1) ≈ 0.018868 s
Por lo tanto, la constante de tiempo es, aproximadamente, 18.87 ms
Os dejo una simulación realizada en LTSpice:
| Problema 2: Transitorios de 1º Orden | |||||||||
|

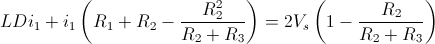
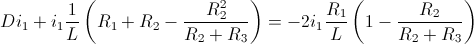
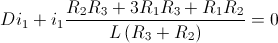
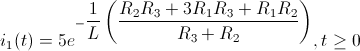









0 comentarios:
Publicar un comentario