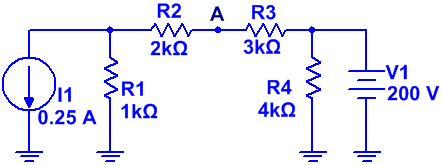
Ej10. Dado el circuito de la figura:
Obtener la tensión VA aplicando el principio de superposición.
El ejercicio nos pide obtener el valor de la tensión VA aplicando el teorema de superposición, es decir, evaluaremos el circuito por cada fuente independiente.
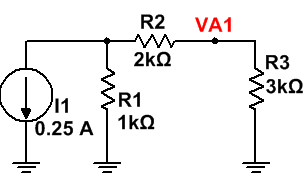
· Fuente de Intensidad Independiente.
Vamos a empezar con la fuente de intensidad independiente, debemos anular la fuente de tensión, para ello, la transformamos en un corto circuito.
Vamos a obtener la intensidad I2 (corriente que circula por los resistores R2 y R3) aplicando un divisor de intensidad:
· I2 = - [R1/(R1 + R2 + R3)]·I1
Y ya estamos en disposición de obtener el valor de la tensión del punto A teniendo en cuenta solo la presencia de la fuente independiente de intensidad mediante la Ley de Ohm:
· VA1 = I2·R3 = - [R1·R3/(R1 + R2 + R3)]·I1
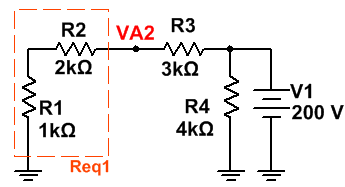
· Fuente de Tensión Independiente.
Ahora, debemos anular la fuente de intensidad, para ello, la transformamos en un circuito abierto.
El circuito equivalente con el que podemos trabajar es el siguiente:
Donde:
· Req1 = R1 + R2
Y ya estamos en disposición de obtener el valor de la tensión del punto A teniendo en cuenta solo la presencia de la fuente independiente de tensión mediante un divisor de tensión:
· VA2 = [Req1/(Req1 + R3)]·V1 = {Req1 = R1 + R2} = [(R1 + R2)/(R1 + R2 + R3)]·V1
Una vez obtenido el comportamiento del punto A con cada fuente independiente por separado, estamos en disposición de resolver el problema, simplemente sumando sus resultados:
· VA = VA1 + VA2 = - [R1·R3/(R1 + R2 + R3)]·I1 + [(R1 + R2)/(R1 + R2 + R3)]·V1 = [ - I1·R1·R3 + (R1 + R2)·V1 ]/(R1 + R2 + R3)
Sustituimos valores para obtener la solución a este problema:
· VA = [- 0.25·1·103·3·103 + (1·103 + 2·103)·200]/(1·103 + 2·103 + 3·103) = - 25 V
Por lo tanto, la tensión del punto A es de, VA = - 25 V.

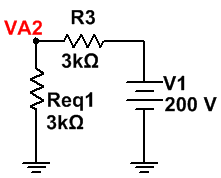




0 comentarios:
Publicar un comentario