Ej3. Consideramos el espacio muestral de un experimento aleatorio en el que todos los sucesos elementales son igualmente probables:
Ω = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}
Y los sucesos S1 = {1, 2, 3, 4} y S2 = {1, 3, 5, 7, 9}.
Calcular:
c) P(S1 U S2)
d) P(S1 ∩ S2)
e) P(S1|S2)
f) P(S2|S1)
El enunciado nos indica que todos los elementos del espacio muestral son igualmente probables, por lo que la probabilidad de cada elemento vendrá dada por la expresión:
Siendo k el elemento del espacio muestral y N el número total de elementos del espacio muestral.
En este caso, el número total de elementos del espacio muestral es N = 12.
Por lo tanto la probabilidad de cada elemento del espacio muestral es:
Con las consideraciones anteriores, pasamos a resolver los distintos apartados.
Apartado a)
La probabilidad de un suceso, es la suma de probabilidades de los elementos de dicho suceso.
En el apartado nos pide el complementario. Se usa la propiedad del complementario:
Apartado b)
Se sigue el mismo razonamiento que en el Apartado a) pero para el suceso S2.
Apartado c)
En este apartado nos pide la probabilidad de unión entre ambos sucesos, es decir, los elementos que estén en el suceso S1 o el el suceso S2 o en ambos.
Esto queda de tal manera:
La probabilidad del elemento intersección corresponde a los siguientes elementos:
Sustituimos valores para resolver este apartado:
Apartado d)
Este apartado nos piden resolver la probabilidad de la intersección entre los dos sucesos. Es decir, los elementos que estén en el suceso S1 y también estén en el suceso S2.
Apartado e)
Probabilidad condicional:
Sustituimos considerando los resultados de los apartados anteriores, obteniendo la solución de este apartado:
Apartado f)
Probabilidad condicional, similar al apartado anterior:
Sustituimos considerando los resultados de los apartados anteriores, obteniendo la solución de este apartado:


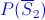
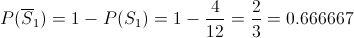
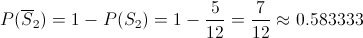
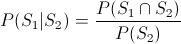
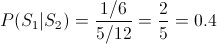





0 comentarios:
Publicar un comentario