Ej2. Sabiendo que:
· P(B) = 1/4.
· P(A∩B) = 1/10.
Calcular:
a) P(A|B).
b) P(B|A).
Apartado a)
Probabilidad condicional:
Apartado b)
El razonamiento es igual que en el apartado a),
· Hay que tener en cuenta que: P(A∩B) = P(B∩A) = 1/10.
Apartado c)
Probabilidad condicional:
Sustituimos valores para obtener la solución a este apartado:
Apartado d)
Probabilidad condicional, similar al apartado anterior:
Sustituimos valores para obtener la solución a este apartado:

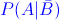
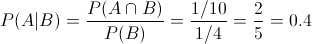

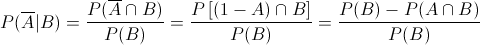
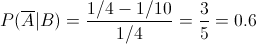






2 comentarios:
hola, en los apartados d, e f... has puesto como pregunta p(AnB) y despues, en la resolucion, calculas el condicional. Creo que esta equivocado.
Buenas:
Efectivamente, los apartados d) y e) estaban erróneos, el f) está bien.
Ya están corregidos, de todas maneras, la solución para los apartados anteriormente mencionados eran:
· P(#A∩B) = P[(1-A)∩B] = P(B)-P(A∩B)= 1/4-1/10 = 0.15 = 3/20.
· P(A∩#B) = P[A∩(1-B)] = P(A)-P(A∩B)= 1/3-1/10 = 7/30.
Gracias por advertirme del error.
NOTA: El signo # quiere denotar negación.
Publicar un comentario