Ej9. Consideramos una familia con dos hijos, suponemos que cada hijo tiene la misma probabilidad de ser niño o niña. ¿Cuál es la probabilidad de que ambos hijos sean niños?, dado qué:
a) El hijo mayor es niño.
b) Por lo menos uno de los dos hijos es niño.
c) Ambos hijos sean niños teniendo en cuenta que algún hijo sea ya niño.
El espacio muestral del problema será:
Ω = {Niño-Niño, Niño-Niña, Niña-Niño, Niña-Niña}
Por lo tanto, tenemos 4 elementos del espacio muestral. El enunciado también nos indica que la probabilidad de que sea niño o niña es la misma, por lo tanto 1/4.
Apartado a)
Definimos los sucesos:
· A Ξ “Sea dos niños”
· B Ξ “Hijo mayor niño”
El suceso A, tendrá un subconjunto del espacio muestral compuesto por:
A = {Niño-Niño}
Al tener sólo un elemento, la probabilidad del suceso A es de ¼.
Así mismo, el suceso B, tendrá un subconjunto del espacio muestral compuesto por:
B = {Niño-Niño, Niño-Niña}
La probabilidad del suceso B es la suma de probabilidades de sus elementos que lo componen:
P(B) = 1/4 + 1/4 = 1/2
Este apartado, nos pide la probabilidad de que ambos hijos sean niños teniendo en cuenta, que el hijo mayor sea niño.
Es una probabilidad condicional.
· P(A|B)
El subconjunto muestral de la intersección de los sucesos A y B es.
P(A ∩ B) = {Niño-Niño}
La probabilidad de la intersección de ambos sucesos es la suma de probabilidades de sus elementos que lo componen, en este caso sólo lo compone un elemento, por lo tanto su probabilidad es de ¼.
Una vez obtenidos los datos, sustituimos los valores en la expresión de probabilidad condicional para resolver este apartado:
Apartado b)
Definimos los sucesos:
· B Ξ “Uno de los dos hijos sea ya niño”
El suceso B, tendrá un subconjunto del espacio muestral compuesto por:
B = {Niño-Niño, Niño-Niña, Niña-Niño}
La probabilidad del suceso B es la suma de probabilidades de sus elementos que lo componen, teniendo en cuenta que la probabilidad de cada elemento es de 1/4:
P(B) = 1/4 + 1/4 + 1/4 = 3/4
Apartado c)
Definimos los sucesos:
A Ξ “Sean dos niños”
B Ξ “Uno de los dos hijos sea ya niño”
El suceso A, tendrá un subconjunto del espacio muestral compuesto por:
A = {Niño-Niño}
Al ser sólo un elemento el suceso A, su probabilidad es de ¼.
La probabilidad del suceso B se obtuvo en el apartado anterior Apartado b), dando el siguiente valor:
P(B) = 1/4 + 1/4 + 1/4 = 3/4
Este apartado, nos pide la probabilidad de que ambos hijos sean niños teniendo en cuenta que algún hijo sea ya niño.
Es una probabilidad condicional.
· P(A|B)
El subconjunto muestral de la intersección de los sucesos A y B es:
P(A ∩ B) = {Niño-Niño}
La probabilidad de la intersección de ambos sucesos es la suma de probabilidades de sus elementos que lo componen, en este caso sólo lo compone un elemento, por lo tanto su probabilidad es de ¼.
Una vez obtenidos los datos, sustituimos los valores en la expresión de probabilidad condicional para resolver este apartado:

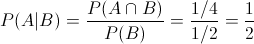
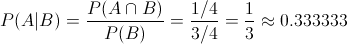




7 comentarios:
Buenas tardes, tengo una duda, a ver,se supone que los niños, tienen la misma probabilidad de ser niño que niña, con lo cual, la probabilidad de ser niño ó niña es 1/2 no?, no veo claro porque dice que es 1/4.
Gracias!
Buenas:
Cierto, la probabilidad por separado de ser niño o niña es la misma, por lo tanto es de 1/2, pero en este ejercicio el evento es por parejas.
Es por ello que debemos confeccionar el espacio muestral del experimento por parejas dónde se puede apreciar que tenemos cuatro eventos.
Por lo tanto, la probabilidad de que salga cualquiera de las parejas es de 1/4.
Un saludo y gracias por tu comentario.
queria agradecer la labor de personas como tu que hacen que personas que necesitan metodos de aprendizajes, diferentes a los didacticos expuestos en clase, sea muy facil y tambien consigues que halla una minima esperanza como en mi caso que afronto un examen de recuperacion. Chapó por ti. eternamente agradecido.
Perdona, creo que se ha equivocado en este ejercicio.
-En el a) ya responde a la pregunta en la probabilidad de B Ξ “Hijo mayor niño”, ya que eso es lo que pregunta éste apartado, que da 1/2;
-EN el b) se equivoca con respecto a que pregunta y que es lo que responde. El resultado que usted pone al final de b) es la probabilidad de que sean dos niños DADO que unos de los dos hijo ya sea niño, que la respuesta es 1/3 como pone ahí. Pero lo que pregunta en este apartado b) no es eso, es que averiguemos la probabilidad de que al menos uno de los dos hijos sea niño que da 3/4.
SALUDOS
Buenas Guille:
Vamos por apartados:
· Apartado a): La probabilidad que piden es una probabilidad condicional, y el apartado está descrito y desarrollado paso a paso de como obtener el resultado.
· Apartado b): Es cierto que lo que pedía el enunciado del problema no corresponde, en parte, con la solución. Esto es debido a que hace tiempo, tuvimos un problema muy serio con el servidor que nos servía para almacenar las expresiones matemáticas que puedes ver.
Tuvimos que reestructurar y volver a escribir gran parte de los problemas. Es por ello que seguramente, habrán problemas incompletos como este en cuestión. Espero que se localicen y se adviertan para que podamos arreglarlos de la manera más rápida posible.
Como ves, ya está todo solucionado, se han creado tres apartados y en cada uno, está su solución desarrollada para que no haya ningún tipo de confusión.
Muchas gracias por tú comentario y por avisarme, un saludo.
Le agradecería que me respondiera a una pregunta. ¿Qué diferencia existe entre "Posibilidad Condicional" y el "Teorema de Bayes"?
Muchas gracias
Buenas:
Vamos a ver, el Teorema o Regla de Bayes, es una probabilidad condicional de varios sucesos, de la siguiente manera:
Sean A1, ..., An sucesos mutuamente excluyentes y exhaustivos con P(Ai) > 0 para cada Ai. Sea B cualquier suceso con P(B) > 0.
Entonces, se define Regla de Bayes:
· P(Ak|B) = [ P(B|Ak)·P(Ak) ]/[Σ( P(B|Ai)·P(Ai) )]
Mientras que en una probabilidad condicional, solo entran en juego dos elementos, por decirlo de otra forma, si el Teorema de Bayes solo entran en juego dos sucesos, estaríamos hablando de una probabilidad condicional.
Un saludo.
Publicar un comentario