Ej2. Sea Y una variable aleatoria continua que tiene la siguiente función de densidad:
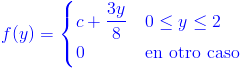
Hallar:
a) El valor de c para que f(y) sea una función de densidad.
b) Obtener la función de distribución.
c) Calcular: P(1 ≤ Y ≤ 1.5).
d) Calcular: P(Y > 1).
Apartado a)
Empleamos la expresión de función de densidad de probabilidad:
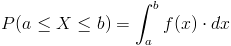
Para los intervalos expuestos en el enunciado del problema, en este caso:
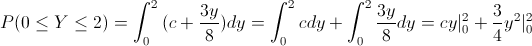
Operando, obtenemos:
2·c + 3/4
Para que una variable aleatoria continua posea una función de densidad de probabilidad, tienen que cumplirse las siguientes condiciones:
1. f(x) > 0,...para todo x.
2.
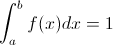
La función f(y) es mayor que cero, por lo que nos queda, satisfacer la primera condición:
2·c + 3/4 = 1
Y así, obtenemos el valor de c y la solución del problema, para que f(y) sea una función de densidad de probabilidad, el valor de c es de 1/8.
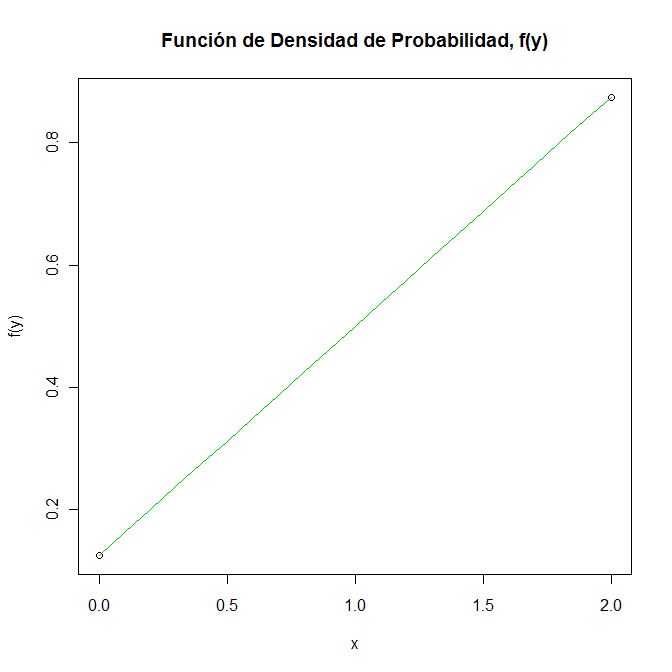
Por lo tanto, la función de densidad de la variable aleatoria continua Y queda:
La representación gráfica de la función de densidad de probabilidad, f(y), se muestra a continuación:
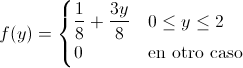
Apartado b)
Empleamos la expresión de función de distribución acumulada:
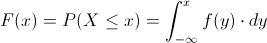
En nuestro caso, el intervalo que tenemos que realizar cálculos es 0 ≤ Y ≤ 2:
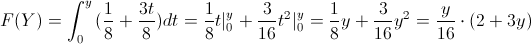
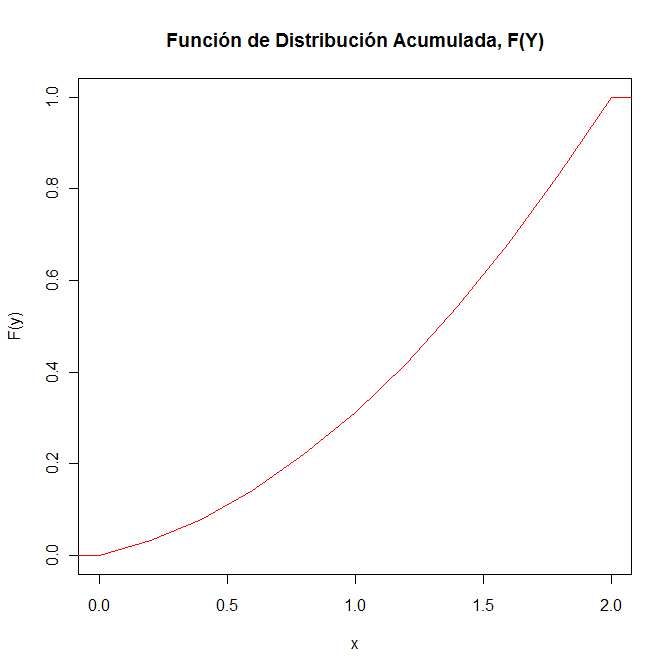
Ya que si y < .0, la función de distribución es 0, y si y > 2, la función de distribución es 1, por lo tanto, la función de distribución acumulada queda tal y como se muestra a continuación:
La representación gráfica de la función de distribución acumulada F(Y) se muestra en la siguiente figura:
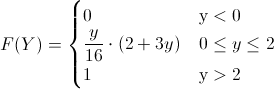
Para calcular la probabilidad de este apartado, empleamos la función de distribución acumulada tal y como se muestra a continuación:
P(1 ≤ Y ≤ 1.5) = F(1.5) - F(1) = (1.5/16)(2 + 3·1.5) - (1/16)(2 + 3) = 19/64
Apartado d)
Para calcular la probabilidad que nos piden en este apartado, al igual que el anterior, hacemos uso de la función de distribución acumulada:
P(Y > 1) = 1 - P(Y ≤ 1) = 1 - F(1) = 1 - (1/16)(2 + 3) = 11/16
7 comentarios:
Que buen ejercicio para entender sobre VAC, lastima que no se ve las funciones!!! saludos
Hola!, en el apartado d), la solución no es 11/16 en vez de 11/64?
Muchas gracias por tu trabajo, me esta siendo de gran ayuda.
Buenas:
Efectivamente, la solución en el apartado d) es 11/16. Ha sido una errata a la hora de escribirla.
Gracias por el apunte y tu comentario, me alegro de que te sea de utilidad los contenidos que exponemos en el blog.
Un saludo.
Hola,me han dado formularios y tablas para resolver los problemas y no veo que usted las utilice,son del tipo areas bajo la curva normal tipificadas de 0 a z valores criticos de la distribucion t de student distribucion ji-cuadrado valores criticos de la dsitribucion F con distintos alfas contrastes de hipotesis sobre poblaciones normales cartas de control....etc
¿donde deberia de usarlas?
Gracias
Un saludo
Buenas:
Si te vas al apartado principal de Estadística, verás que existen capítulos expresos de las tablas que se utilizan en este blog (que por cierto no son pocas). También están disponibles para su descarga.
Lo que pasa que se utilizan en el momento adecuado, en este caso (problema), no es necesario.
Ya que aquí lo que debemos obtener son probabilidades mediante la distribución acumulada.
Un saludo y gracias por tu comentario.
Che, una pregunta. Cual es la diferencia entre funcion de distribucion y funcion de densidad? Aun me lio bastante. Gracias de antemano y felicides por el blog.
Buenas Emmanuel:
La función de densidad es aquella que describe todos los valores de la variable aleatoria mientras que la función de distribución acumulada, asocia a cada valor de la variable aleatoria, la probabilidad acumulada hasta ese valor.
En otras palabras, la función de densidad nos indica el comportamiento de la variable aleatoria mientras que la función acumulada nos ofrece el valor acumulado en un intervalo dado.
Un saludo.
Publicar un comentario